エイトクイーンとは?
駒の移動できる場所を利き筋と呼びます。

チェスのクイーンでは、利き筋が縦、横、斜めのラインのマスです。
エイトクイーンとは、チェスの盤面においてお互いに利き筋にならないように8コのクイーンを配置するパズルのことを言います。
Pythonで表現すると
「Visual Studio Code」で記述した場合こちらが綺麗に表示されました。
#例えばq[1]は、一列目にはQがどの行に配置されているかを表す
#エイトクイーンは、お互いにとられないように配置するため、同じ行、列、斜めのラインに配置されることはない
q = [0]*8#列を表すインデックスとなる
pattern = 0
def put_q(x):
q[x] = 0
global pattern
while True:
c = chk_q(x, q[x])#q[x]より以前のものと比較して置ける場所か判定
if c == True:#おける場所だった場合、
if x == 7:#最後の列だった場合
pattern += 1#パターンとして追加
prt_q()#表示させる
break
else:
put_q(x+1)
q[x] += 1
if q[x]>=8:#x列目のどこにも置けなかった場合
break
def chk_q(x,y):
i = 0
while (i < x):
if q[i]!=y and q[i]!=y-x+i and q[i]!=y+x-i:
i+=1
else:
ret = False
return ret
ret = True
return ret
def prt_q():
print(f"\nパターン{pattern}")
for i in range(8):
for j in range(8):
if q[j]==i:
print(" Q ", end="")
else:
print(" ・ ", end="")
print("")
put_q(0)
エディッタに応じて、関数prt_q()のprint部分を変更して綺麗にに、エイトクイーンのパターン一覧が表示されるようにしてください。
プログラムコード解説
このプログラムコードでは、関数を再帰呼び出しを用いてエイトクイーンを表現しています。
「関数put_q(x)」では、このエイトクイーンのメインとなる関数で、再帰呼び出しを行って最終的には、「関数chk_q(x,y)」を用いて全行全列でエイトクイーンが成立する配置を調べます。
「関数chk_q(x,y)」では、x列目のy行目が配置できるましょかを調べてくれます。配置することができる場合は、Trueを返します。配置できない場合は、Falseを返します。
「関数prt_q」では、確定したパターンを表示します。
put_q(0)から始まるこのプログラム。
0列目が0行目に配置された状態から1列目以降をエイトクイーンのルールに従って行を決めていく。
下のように、順に左から配置場所を決めていきます。
(※0列0行目から始まる)
1列目は、0列目の利き筋に入らないようにいっこは、0列目の利き筋に入らないように1個ずつ上から配置していきます。今回の例だと、1列目は2行目に配置されることが分かります。また、2列目では、0列目のクイーンと1列目のクイーンのクイーンの利き筋に入らないように配置します。今回の例だと、2列4行目に配置されることになります。同じように1列ずつ配置場所を決めていきます。
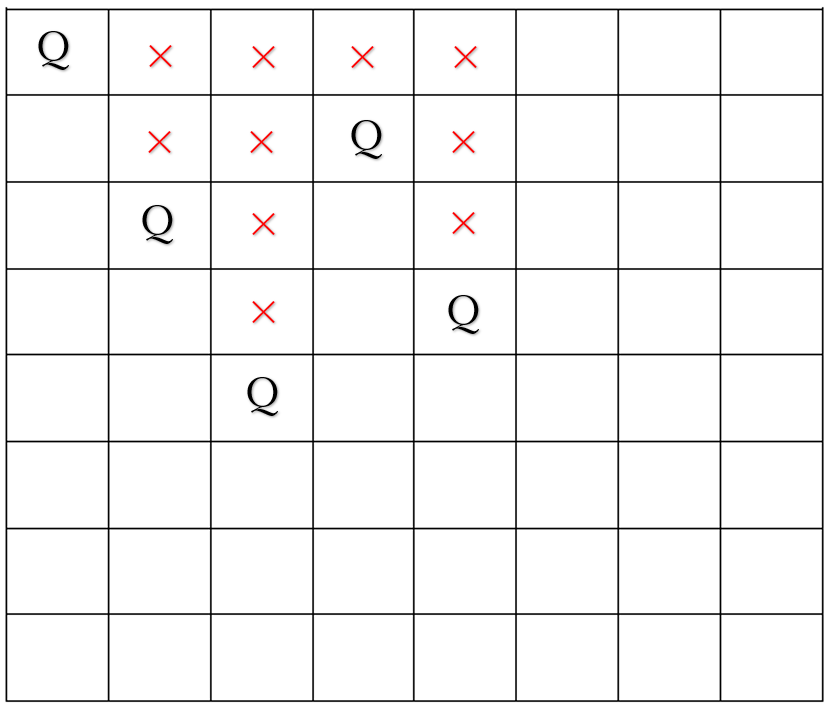
しかし、1列ずつ配置場所を決めていくと問題が起こります。
↓のように、×が一番下の行までいき、5列目では、配置することができないことになります。

この場合は、一つ前の列の行を一段下げるということを行います。
5列目で配置することができなかったため、1つ前の列の配置を1段下げます。
ですが、ここで1段下げる場合もエイトクイーンのルールに従う必要があるので、今回の場合だと
3列1行目に配置されていた×が、3列6行目に配置されることになります。
また、4列3行目に配置されていた×が4列1行目に移動し、5列目は3行目に配置することができました。
このように、調整してクイーンを配置していきます。
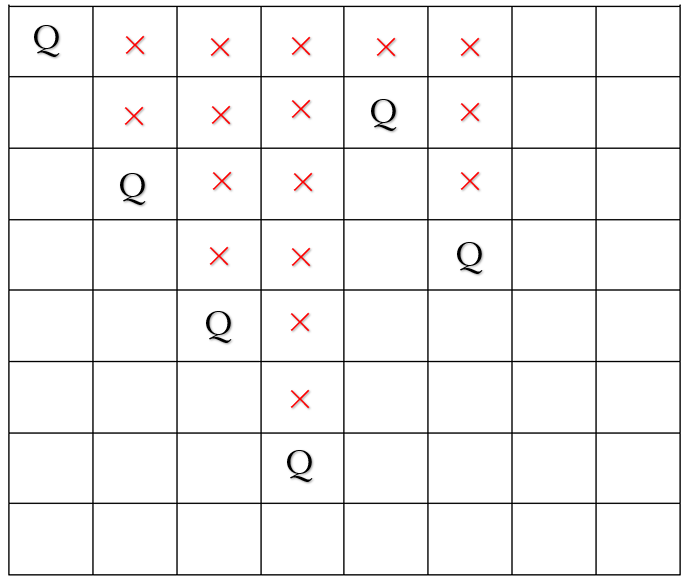
最終的に、7列目まで配置することができた配置がエイトクイーン配置の一つとなります。
エイトクイーンの場合、配置できるのは92通りです。
最初にエイトクイーン配置が決まるのは、
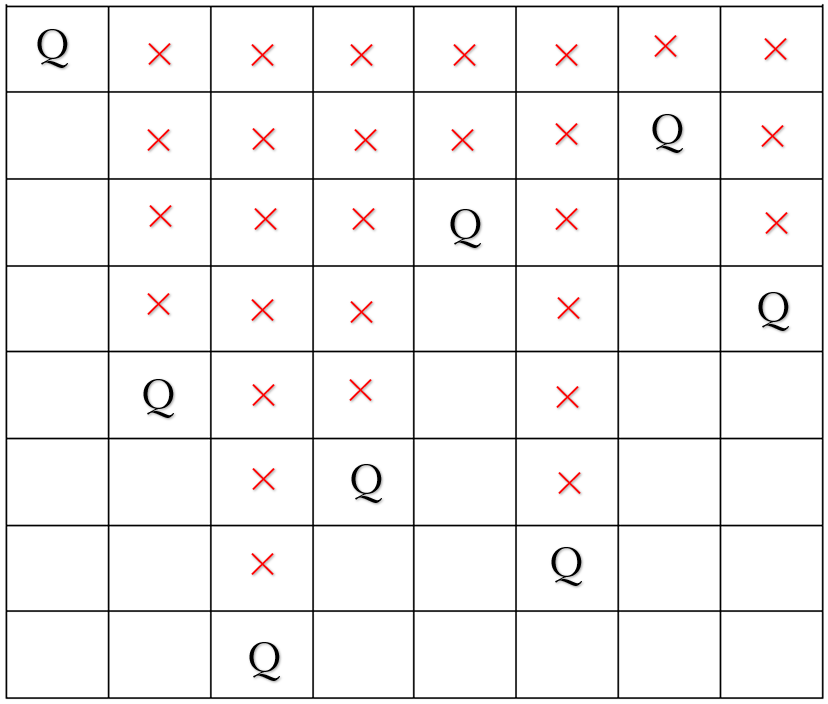
となります。


コメント