 ディジタル回路
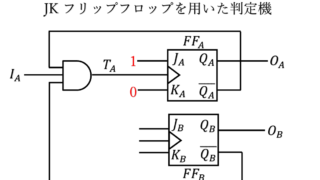
ディジタル回路 [例題解説] JKフリップフロップ回路 判定機問題
ディジタル回路の設計では、フリップフロップを用いた順序回路の解析や設計が重要なテーマとなります。特に、JKフリップフロップを用いた問題は、多くの大学院入試や資格試験で出題される定番の問題です。この記事では、名古屋工業大学の2023年度大学院...
 ディジタル回路
ディジタル回路  就活
就活  大学院
大学院  大学院
大学院  応用情報技術者試験
応用情報技術者試験  院試
院試 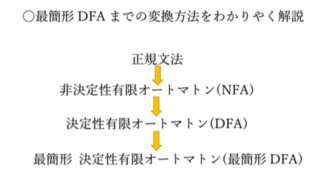 オートマトン
オートマトン  プログラミング
プログラミング  プログラミング
プログラミング  プログラミング
プログラミング  プログラミング
プログラミング  ポイ活
ポイ活  生活
生活  ポイ活
ポイ活  情報数学
情報数学  情報数学
情報数学 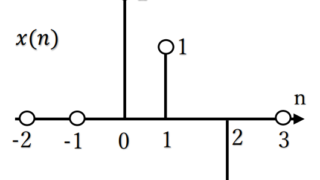 信号処理
信号処理  生活
生活  生活
生活  プログラミング
プログラミング 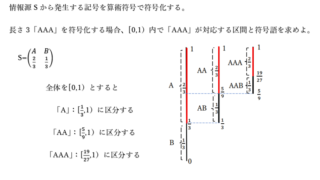 情報数学
情報数学  プログラミング
プログラミング 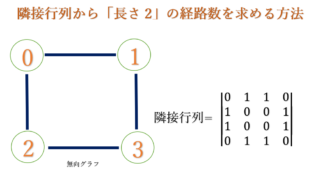 情報数学
情報数学  プログラミング
プログラミング  プログラミング
プログラミング  プログラミング
プログラミング 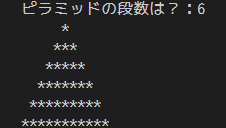 プログラミング
プログラミング 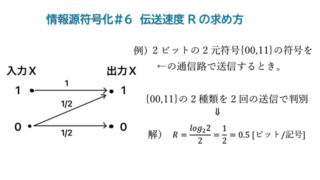 情報数学
情報数学 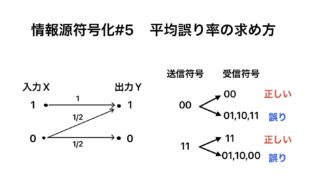 情報数学
情報数学 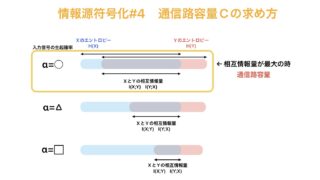 情報数学
情報数学 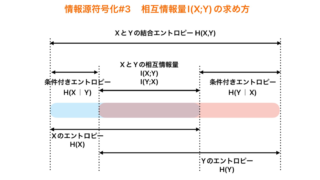 情報数学
情報数学  情報数学
情報数学  情報数学
情報数学