Pythonを使って線形探索のプログラムを考えます
今回は例として、
【3,5,7,9,11,13,15,17,19,21,23,25,27】
の数字列の中から「11」を探し出すプログラムを考えます。
※線形探索法は、(大きい順) または (小さい順) に整列されていなくても、
探索可能ですが、今回は整列済みの数字列を扱います。
線形探索法とは?
探し出したいデータを、探索対象データの先頭から順に探索していく方法。
比較回数| 最小:1回 最大:n回
平均比較回数| (n+1)/2 回
探し出したいデータが、探索対象データの前の方にあると比較回数が少なくて済み、
逆に、後ろの方にあると比較回数が多くなる探索法です。
プログラム例
Pythonで線形探索法をプログラムすると、どうなるか見ていきます。
先ほど、示した数字列 【3,5,7,9,11,13,15,17,19,21,23,25,27】 から、
「11」を探し出すプログラムです。
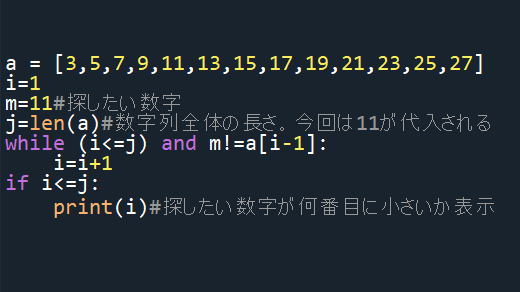
a = [3,5,7,9,11,13,15,17,19,21,23,25,27]
i=1
m=11#探したい数字
j=len(a)#数字列全体の長さ。今回は11が代入される
while (i<=j) and m!=a[i-1]:
i=i+1
if i<=j:
print(i)
数字列を「a」に格納しています。
プログラムの解説
このプログラムを実行すると、「5」が出力されます。
「11」は5番目なので、このプログラムが探索成功されていることが分かります。
上記のプログラムが実行されると、どのような処理が行われるのか見ていきましょう!!
変数の紹介
「i」:端から比較する探索方法なので、どこと比較するかを「i」が表します。
「m」:探索したい数字を代入します。
「j」:数字列全体の長さを表し、これのおかげで「while文」が利用できています。
while文で、端から比較するという処理が行われています。
while文の条件は、 (i<=j) and m!=a[i-1] なので、これが満たしている間はループします。
1回目のループ)「i」には1、「m」には11、「j」には13が代入されています。
「while文」の条件に代入すと、 1<=13 and 11!=3 ということで、
条件を満たすので、中の処理が行われます。
中の処理は、 i=i+1 ということで、「i」が1増えます。
2回目のループ)「i」には2、「m」には11、「j」には 13が代入されています。
「while文」の条件をみたすので、中の処理が行われます。
ここで、i=2+1で3になりました。
3回目のループ)「i」には3、「m」には11、「j」には13が代入されます。
「while文」の条件をみたすので、中の処理が行われます。
ここで、i=3+1で 「i」は4になります。
4回目のループ)「i」には4、「m」には11、「j」には13が代入されています。
今回も、条件をみたすので、iが1増加して、5になります。
5回目のループ) 「i」には5、「m」には11、「j」には13 が代入されたいます。
今回は、条件文に当てはめてみると、
5<=13 and 11!=11 となります。
これは、11!=11となっているので、条件満たしていないことになりますよね。
ということで、5回目ループには入らずに「while文」を抜け出すことになります。
「while文」の下にはif文があって、
i<=jだった場合、「i」を出力するという内容です。
現在の「i」は「5」なので、「5」が表示されます。



コメント