隣接行列について
過去に隣接行列についてまとめたブログがあるので、隣接行列についてはこちらをご覧ください。
↓を参照しておきます。
隣接行列の積をPythonで表現する方法
今回も、この無向グラフを用いて考えていきます。

そのため、隣接行列は↓のようになりますね。

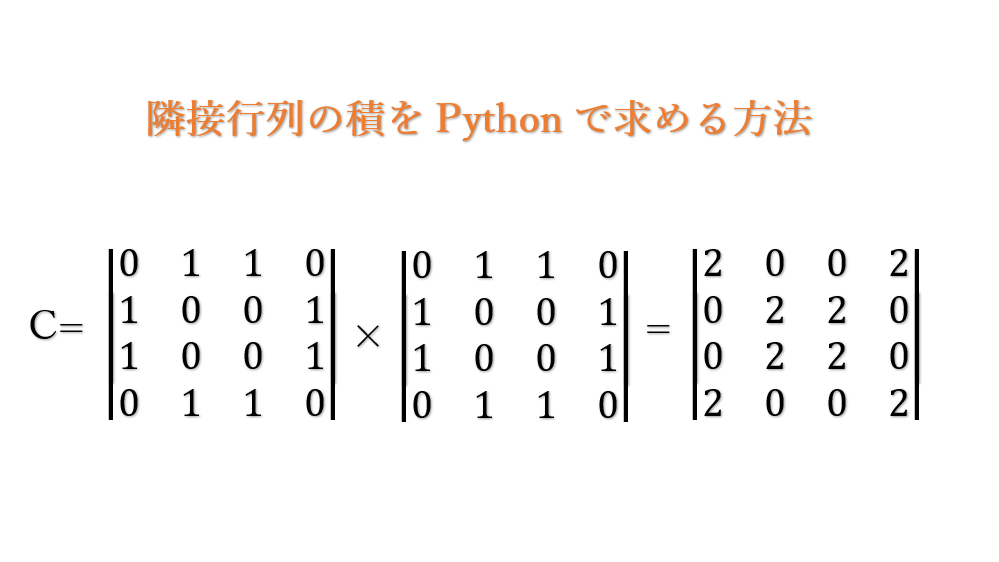
経路数を求めるには、隣接行列の積を求める必要があります。
隣接行列は必ず正方行列となるため、正方行列の積を求める関数「multiply」を作成します。
また、行列計算で用いられる方法である。二重リストを用いて隣接行列Aを表現します。
これらをPythonで表現すると↓のようになります。
N=4#節点数(節点0,1,2,3の4つ)
def multiply(c,a,b):#N次正方行列の積を求める関数
for i in range(N):
for j in range(N):
s=0
for k in range(N):
s+=a[i][k]*b[k][j]
c[i][j]=s
#長さ2の経路数を表す行列Cを作成
C=[[0 for j in range(N)] for i in range(N)]
#隣接行列Aを2重リストを用いて表現
A = [[0,1,1,0],
[1,0,0,1],
[1,0,0,1],
[0,1,1,0]] # 隣接行列 A
multiply(C,A,A) # 行列Cを計算(C=A*A)
#行列Cを表示
for i in range(N):
for j in range(N):
if j == N-1: print(" ",C[i][j])
else: print(" ",C[i][j],end="")
これを実行すると、
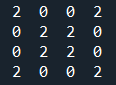

手計算した場合と比較しても、上手くいっていることがわかります。
正常に「長さ2」の経路数が求められています。
「長さ3」の経路数をPythonで求める方法
「長さ3」の経路数を表す行列Fを、隣接行列を用いて手計算で求める場合、
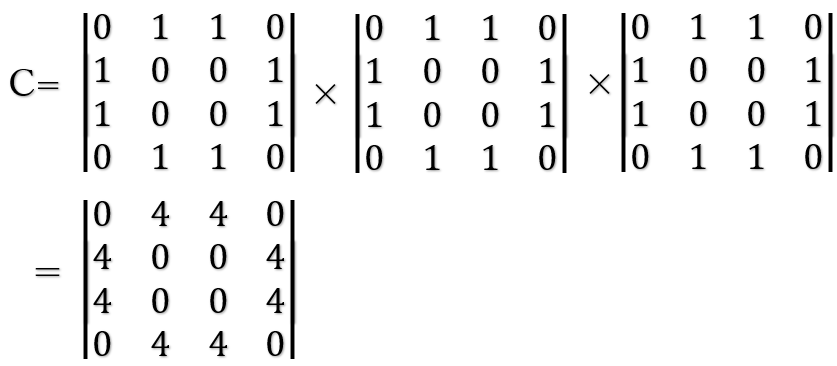
となります。
これを先ほどのPythonプログラムコードを用いて、表現したいと思います。
N次正方行列の積を求めてくれる 関数「multiply」 を使えば、
行列Fも簡単に求められます。
N=4#節点数(節点0,1,2,3の4つ)
def multiply(c,a,b):#N次正方行列の積を求める関数
for i in range(N):
for j in range(N):
s=0
for k in range(N):
s+=a[i][k]*b[k][j]
c[i][j]=s
#長さ2の経路数を表す行列Cを作成
C=[[0 for j in range(N)] for i in range(N)]
#長さ3の経路数を表す行列fを作成
F=[[0 for l in range(N)] for i in range(N)]
#隣接行列Aを2重リストを用いて表現
A = [[0,1,1,0],
[1,0,0,1],
[1,0,0,1],
[0,1,1,0]] # 隣接行列 A
multiply(C,A,A) # 行列Cを計算(C=A*A)
multiply(F,C,A) # 行列Fを計算(F=C*A)
#行列Fを表示
for i in range(N):
for j in range(N):
if j == N-1: print(" ",F[i][j])
else: print(" ",F[i][j],end="")
青字の所が、先ほどのプログラムコードからの変更点です。
行列Fを求めるコードを追加し、表示する2重リストをFに変更しただけですね。
長さ3以降の経路数を表す行列も、同じように求めていくことができます。


コメント