離時間信号は単位インパルス信号の合成で表すことができる。
単位インパルス信号:時刻n=0で1、その他の時刻で常に0となる信号をδ(n)で表す。

単位インパルス信号を図示すると、
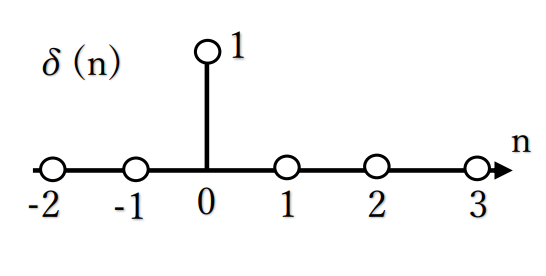
となる。
次の離散時間信号
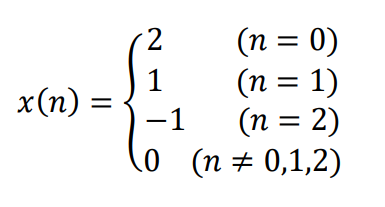
は、単位インパルス信号を用いて次のように表せる。
x(n)=2δ(n)+3δ(n-1)ーδ(n-2)
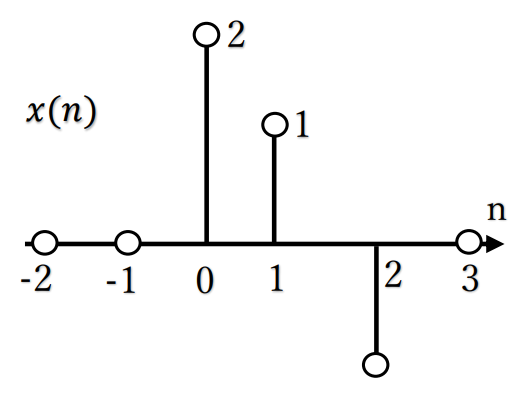
例題を使って信号を図示する方法を確認していきます
[1] x1(n) = δ(n)ーδ(n-1)+2δ(n-2)
離散時間信号を図示すると、
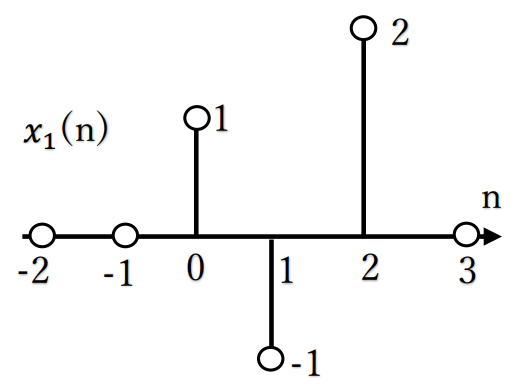
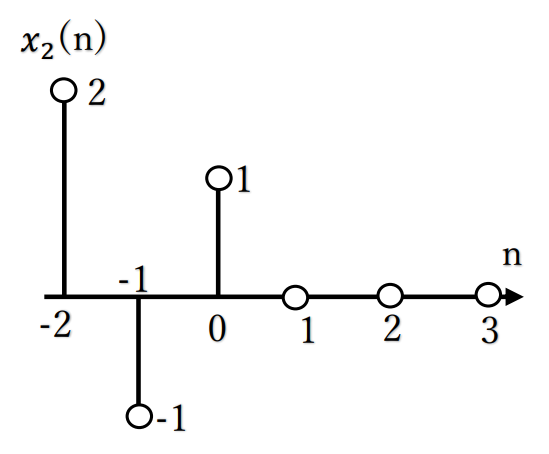
[2] x2(n) = x1(ーn)
= x1(n)をn=0を軸に軸対称したモノ
= 2δ(n+2) ー δ(n+1) +δ(n)
離散時間信号を図示すると、
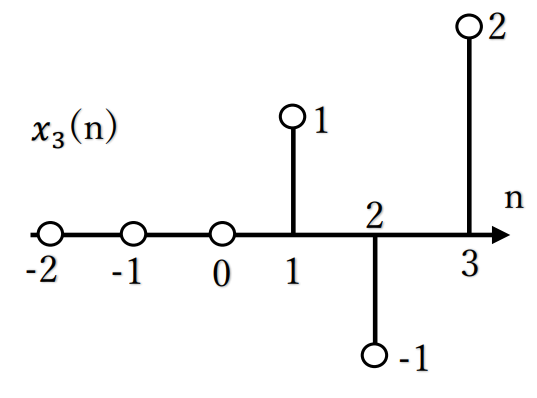
[3] x3(n)=x1(n-1)
=x1(n)を右に1シフトしたモノ
=δ(n-1)ーδ(n-2)+2δ(n-3)
離散時間信号を図示すると、
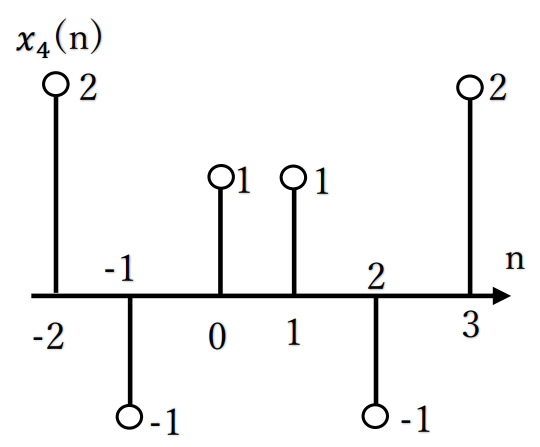
[4] x4(n)=x2(n)+x3(n)
=2δ(n+2) ー δ(n+1) +δ(n)+δ(n-1)ーδ(n-2)+2δ(n-3)
離散時間信号を図示すると、
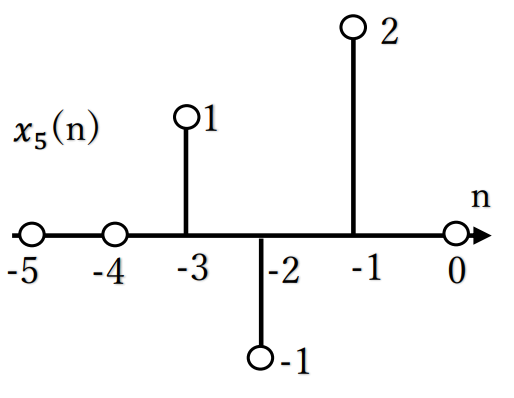
[5] x5(n)=x1( ーn-1)
=x1(n)を右に1シフトして、n=0を軸に軸対称
=δ(n-1)ーδ(n-2)+2δ(n-3) を n=0を軸に軸対称
=2δ(n+3) ーδ(n+2)+δ(n+1)
離散時間信号を図示すると、
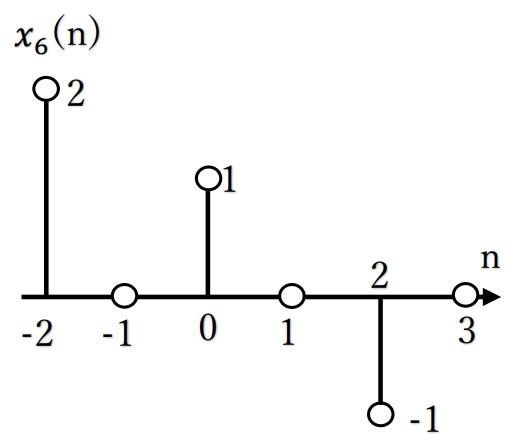
[6] x6(n)= x4(2n)
離散時間信号のため、n=…,-1,0,1,…の整数
n=-1のとき、x4(-2)=2
n=0のとき、x4(0)=1
n=1のとき、x4(2)=-1 となる。
その他のnに整数をいれても0となる
離散時間信号を図示すると、
コメント