本記事では、「正規文法」→「非決定性有限オートマトン」→「決定性有限オートマトン」→「最簡形決定性有限オートマトン」の変換方法をメインに解説します。そのため、各単語についての説明などは他サイトをご紹介することがございますので、ご了承ください。
「正規文法」と「有限オートマトン」について
「正規文法」とは
形式文法の一種。正規文法で生成できる言語は「正規言語」。「正規言語」は「有限オートマトン」で認識可能であるという特徴を持ってます。パターンや文字列の構造を表現するために使用されます。
「正規文法」は「文脈自由文法」の一部です。「文脈自由文法」は「正規文法」よりもより複雑な構造の文字列を表現することができます。「文脈自由文法」が生成する言語は「文脈自由言語」で「プッシュダウンオートマトン」で認識可能という特徴を持ちます。
「正規文法」と「文脈自由文法」については、とても詳しく書かれた記事がありましたので、↓を参考にして下さい。
加えて補足させて頂くと、「正規文法」の生成規則は基本的に
A→aB(非終端記号1文字→非終端記号1文字＋終端記号1文字)
A→a (非終端記号1文字→終端記号1文字)
のどちらかの形式で表現されています。
※参考書、記事によっては「正規文法」を「正則文法」と記されている場合もあります。「正規」と「正則」は同じ意味で扱われているのでご注意ください。
「有限オートマトン」とは
先ほど説明しましたように「正規文法」と密接に関係しており、相互に変換可能な対応関係があります。どちらも「正規言語」の表現手段として使用されます。
「有限オートマトン」についても、とても詳しく書かれた記事がありましたので、↓を参考にして下さい。
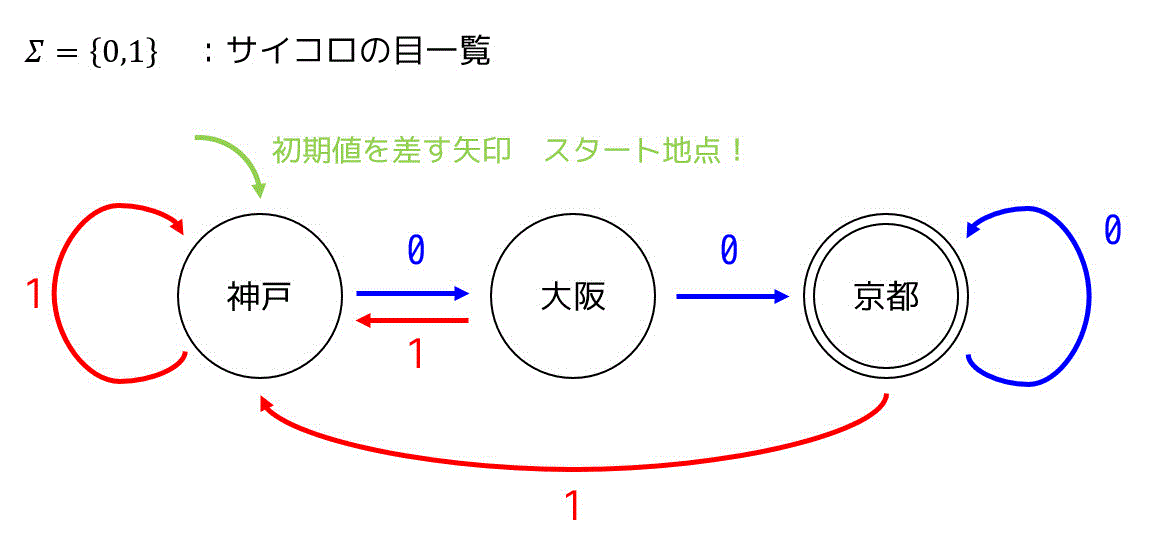
加えて補足させて頂くと、
有限オートマトンには次の2種類あります。どちらも、正規文法で表現できます。
１．決定性有限オートマトン(DFA)
２．非決定性有限オートマトン(NFA)
１．決定性有限オートマトン(DFA)
各状態において、全種類の入力シンボルに対する遷移先状態が必ず一つ存在する有限オートマトンのことです。つまり、どの状態でどんな入力を受け取っても必ず1つの遷移先が決まっています。不必要な入力などがある場合は「ゴミ箱」に遷移する場合があります。
DFAの例1(ゴミ箱なし)
正規文法G1
G1=＜{A,B,C},{a,b},P,A＞
P={A→aB,A→bA,B→aB,B→bC,B→b,C→a,C→b}
※状態A,B,Cはそれぞれq0,q1,q2で表されています。
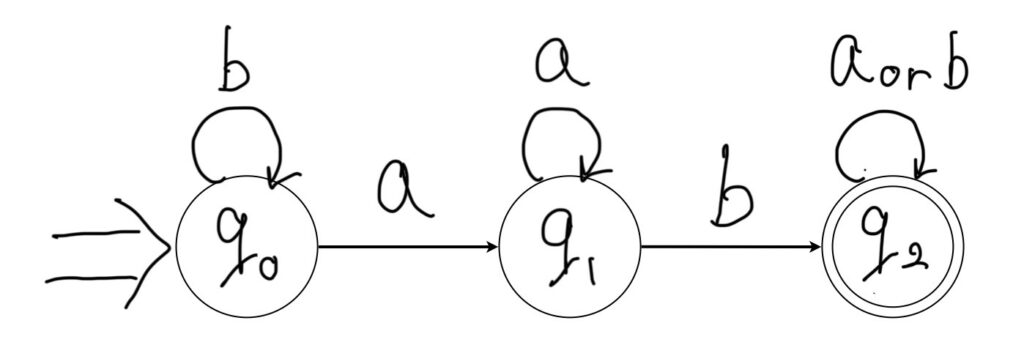
G1が生成する言語を受理する決定性有限オートマトンを示したものです。
各状態に対して入力a,bどちらを入力されてもそれぞれ必ず一つの遷移先が決まっていますね。
DFAの例2(ゴミ箱あり)
正規文法G2
G2=＜{A,B,C},{a,b},P,A＞
P={A→aB,B→aC,C→a,C→b}
※状態A,B,Cはそれぞれq0,q1,q2で表されています。
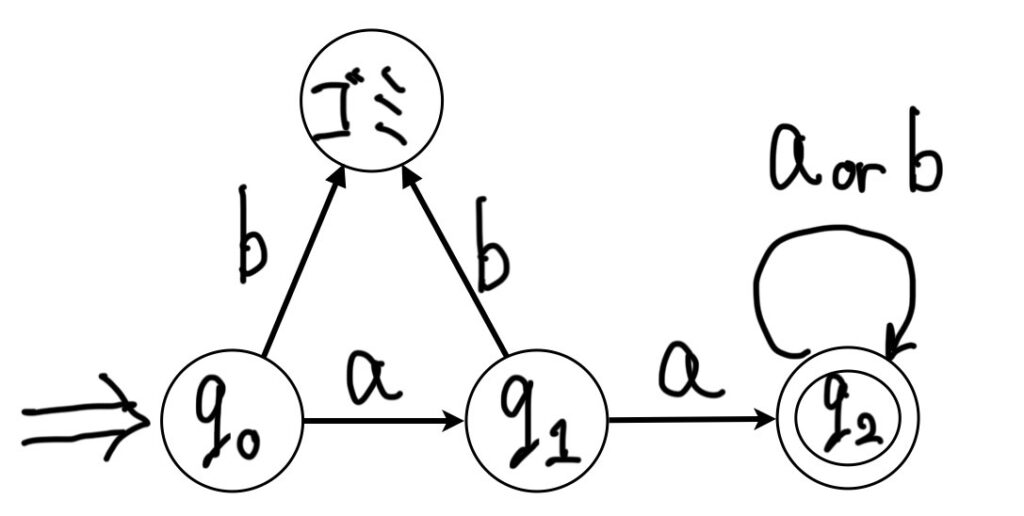
G2が生成する言語を受理する決定性有限オートマトンを示したものです。
G2にはAの状態でbが入力された時の遷移先が示されていませんが、決定性有限オートマトンは全ての状態において全ての入力シンボルに対する遷移先状態が必ず一つ存在するので、明記されていない場合は不要な遷移であるので↑のDFAのようにゴミ箱を用意して、そこに遷移させるように表現します。
２．非決定性有限オートマトン(NFA)
各状態において、各状態においてある入力シンボルに対して複数の遷移先が存在する有限オートマトンのことです。複数というのは、０個以上ということで遷移先がなくてもよいという事です。
NFAの例
正規文法G3
G3＝<{A,B,C,D}{a,b},P,A>
P={A→bB,A→aC,B→aB,B→bB,B→aD,C→aC,C→bD,C→bC}
※状態A,B,C,Dはそれぞれq0,q1,q2,q3で表されています。
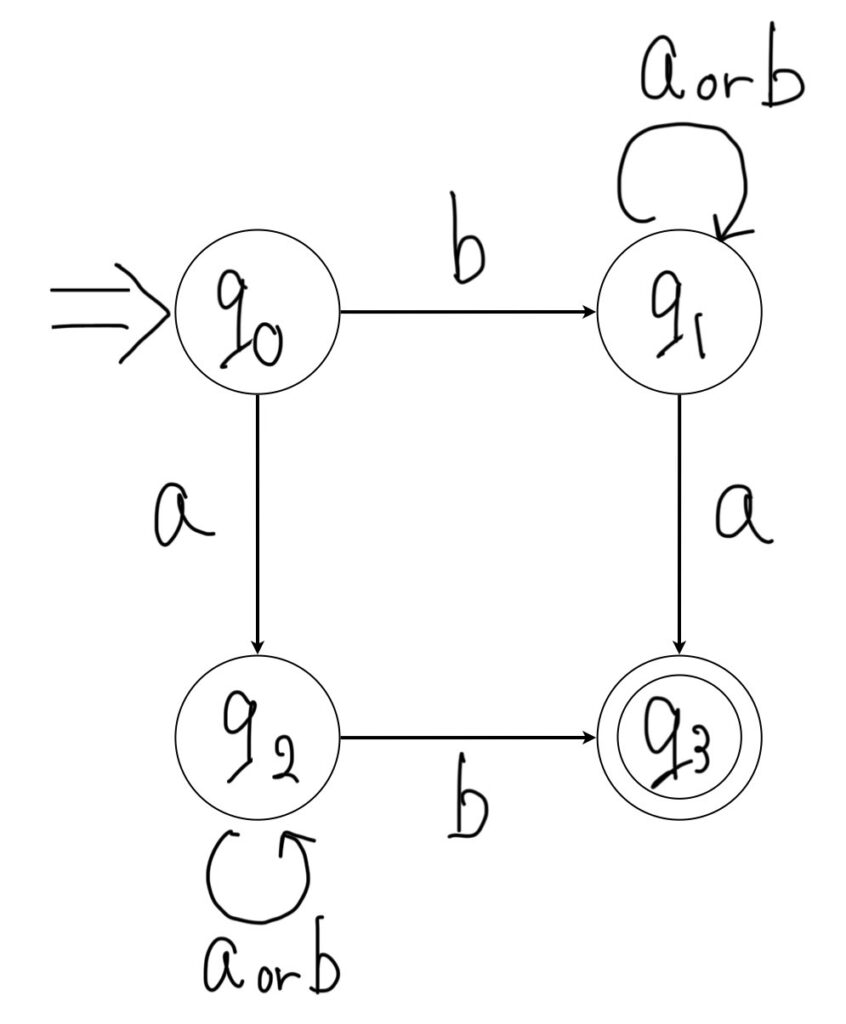
q1の状態でaが入力された時の遷移先としてq1とq2の2通りがあります。
また、q3の状態では入力がなく遷移先が1つもありません。
このように、各状態においてある入力シンボルに対して0個以上の遷移先が存在するのが特徴です。
正規文法→NFA
例題を用いて正規文法からNFAに変換していきます。
例題）
正規文法G1=＜{A,B,C},{x,y},P,A>
P={A→x,A→xA,A→yA,A→xB,B→xC,B→yC,B→x,B→y,C→yC}
からG1が生成する言語を受理する非決定性有限オートマトン(NFA)に変換せよ。
正規文法をG1を詳しくみてみます。
・G1の非終端記号は{A,B,C}
・G1の終端記号は{x,y}
・G1の生成規則は P
・G1の初期状態は A
となっております。
生成規則 P を参考にそれぞれの状態を整理していきます。
まず、状態Aについてです。
状態AはG1で初期状態に設定されています。
「A→x」「A→xA」「A→xB」から
状態Aにxが入力されると、「受理」 か 「状態Aへ遷移」 か「状態Bへ遷移」。
「A→yA」から
状態Aにyが入力されると、「状態Aへ遷移」。
することがわかります。
状態Bについて
「B→xC」「B→x」から
状態Bにxが入力されると、「状態Cへ遷移」 か 「受理」。
「B→yC」「B→y」から
状態Bにyが入力されると、「状態Cへ遷移」 か 「受理」。
状態Cについて
「C→yC」から
状態Cにyが入力されると、「状態Cへ遷移」。
となっています。
現状では「受理」となった場合の状態が無い状態なので自分で作ります。
今回はFinishの頭文字をとり 「状態F」 を受理状態ということにします。
また、有限オートマトンでは受理状態を◎で表現します。
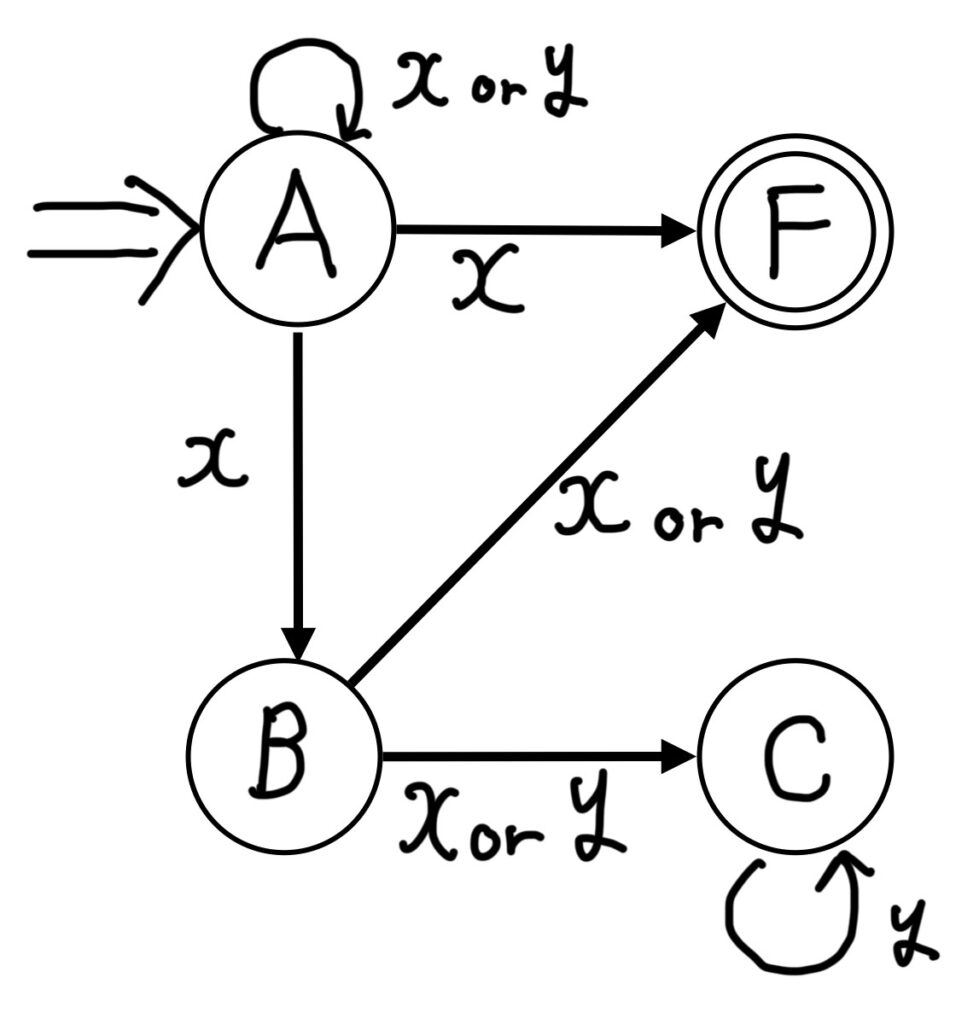
状態A,B,C,Fの入力と遷移先を非決定性有限オートマトンで表現します。
状態Aは初期状態なので、無条件で⇒で示されています。
状態Aでxが入力されると、状態A,B,Fに遷移。
状態Aでyが入力されると、状態Aに遷移。
状態Bでxが入力されると、状態C,Fに遷移。
状態Bでyが入力されると、状態C,Fに遷移。
状態Cでyが入力されると、状態Cに遷移。
というように、全ての状態において正規文法を非決定性有限オートマトン(NFA)で表現できています。
※「状態Cでのxの入力」については正規文法で明記されていないので、表現する必要がありません。
NFA→DFA
次は非決定性有限オートマトン(NFA)から決定性有限オートマトン(DFA)に変換したいと思います。
１．状態遷移表を作成
まずは、先ほど作成したNFAの状態遷移表を考えていきます。
状態遷移表は↓を参考に作成してみてください。
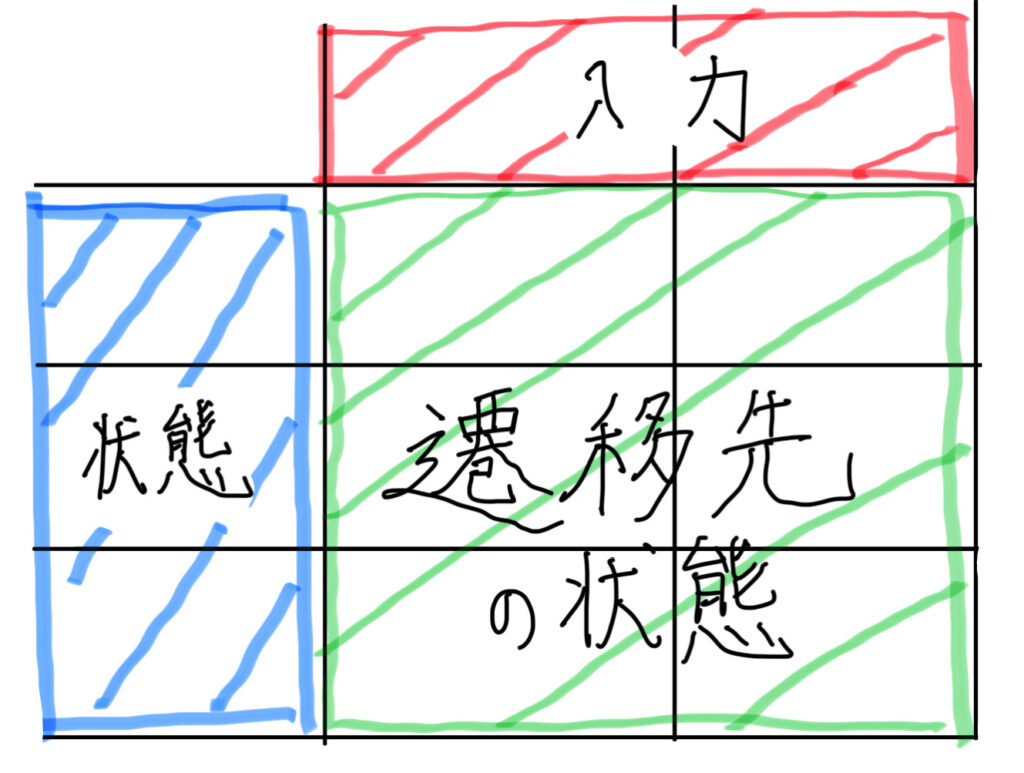
表側(青い箇所)には「状態」を書いてください。
※初期状態には「⇒」
受理状態には「*」を記しておいてください。
表頭(赤い箇所)には「入力」を書いてください。
表体(緑の箇所)には「遷移先」を書いてください。
※状態に対して入力がない場合は遷移先がないということなので、
「Φ」を記しておいてください。
今回の例題で確認してみましょう。
まずは、表体(青い箇所)を作成します。
状態の種類は「A」「B」「C」「F」の4種類ですね。
「A」に関しては、初期状態なので「⇒」を書きます。
「F」に関しては、終了状態なので「*」を書きます。
次に、表頭(赤い箇所)を作成します。
入力は「x」「y」の2種類。
最後に、表体(緑の箇所)を作成します。
「A」に対して「x」が入力されたら、「A,B,F」に遷移。
「A」に対して「y」が入力されたら、「A」に遷移。
「B」に対して「x」が入力されたら、「C,F」に遷移。
「B」に対して「y」が入力されたら、「F」に遷移。
「C」に対して「x」が入力されたら、遷移先なし。
「C」に対して「y」が入力されたら、「C」に遷移。
「F」に対して「x」「y」が入力されたら遷移先なし。
これらの情報を状態遷移表にあてはめます。
※「遷移先なし」のとこは「Φ」
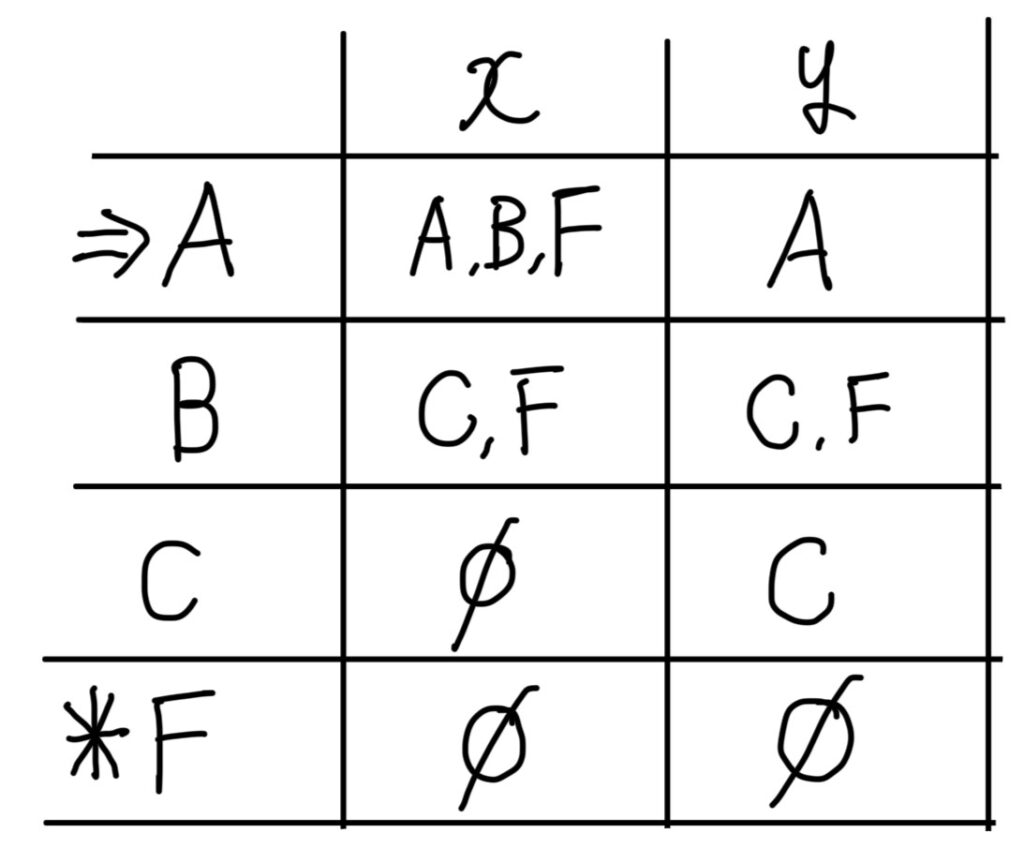
となります。
これが、NFAの状態遷移表となります。
２．NFAの状態遷移表→DFAの状態遷移表
次は、このNFAの状態遷移図からDFAの状態遷移図へと変換してみたいと思います。
NFAでは、1つの入力に対して複数の状態に遷移することができますが、DFAでは1つの入力に対して1つの状態にしか遷移しません。そのため、NFAの状態遷移表における遷移先を1つのまとまり(状態の集合)として考えます。このまとまりがDFAの１つの状態として扱います。
NFAの現在の遷移先の状態集合に入力されたときに、到達可能なすべての状態の集合を計算し、それをDFAの遷移先とします。この操作をすべての状態と入力について繰り返すことで、DFAの状態遷移表を埋めます。
例えば、NFAに「状態A」が「入力x」に対して「状態B,C」に遷移するとします。この場合、DFAでは「{A}」から「入力x」に対して「{B,C}」という状態に遷移すると記述します。この手順をすべてのNFAの初期状態と遷移先状態集合について繰り返し、DFA全体の遷移表を構築します。
といっても、わかりづらいと思うので例題を用いて確認します。
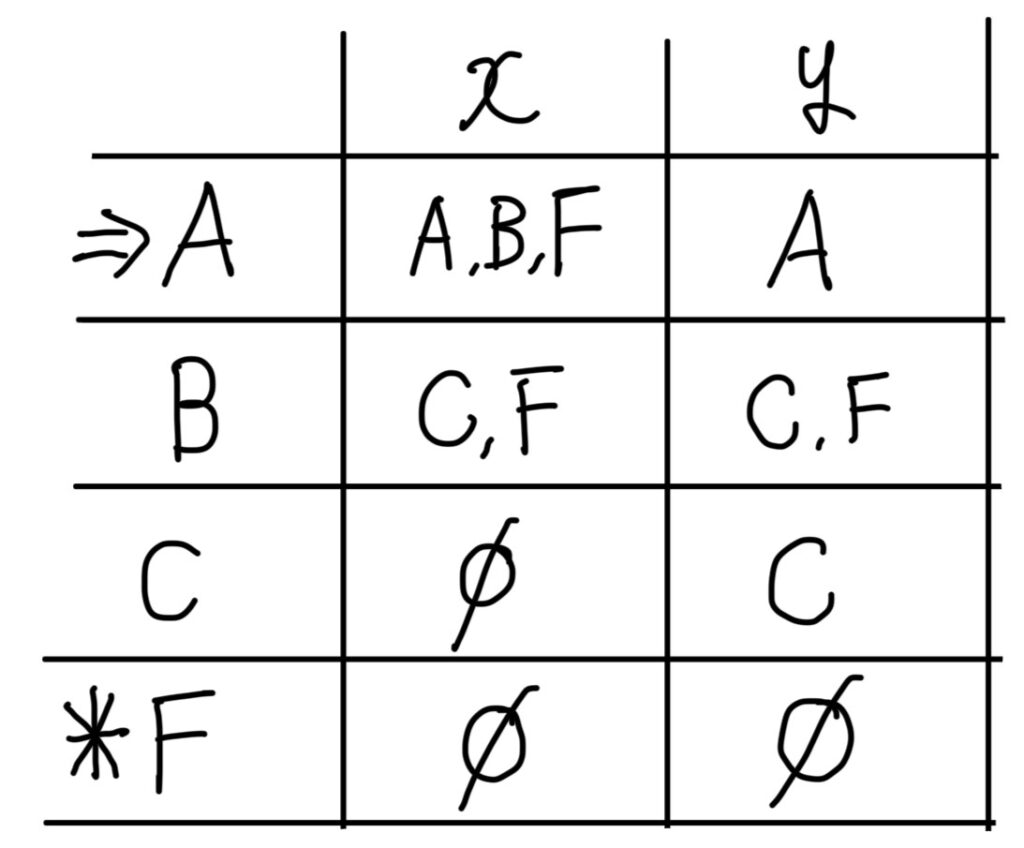
まずは、初期状態Aについて考えます。
NFAの状態遷移表では、状態「A」は「x」が入力されると、状態「A」「B」「F」に遷移します。
これをDFAでは、状態「A」では「ｘ」が入力されると、状態「A,B,F」に遷移すると考えます。
状態「A」で「y」が入力されると、状態「A」に遷移します。
次に、状態「A,B,F」を考えます。
この状態は「A」「B」「F」を集合として集めて考えた状態です。
なので、状態「A,B,F」で「x」が入力されると、「A」で「x」が入力された時の遷移先状態。「B」で「x」が入力された時の遷移先状態。「F」で「x」が入力された時の遷移先状態 の集合として考えます。
「A」の時「x」が入力されると「A,B,F」に遷移。
「B」の時「x」が入力されると「C,F」に遷移。
「F」の時「x」が入力されると「Φ」。
したがって、「A,B,F」は「x」が入力されると「A,B,C,F」に遷移します。
※状態「F」は受理状態ということになっているので
「F」が入る状態には「＊」を記しておいてください。
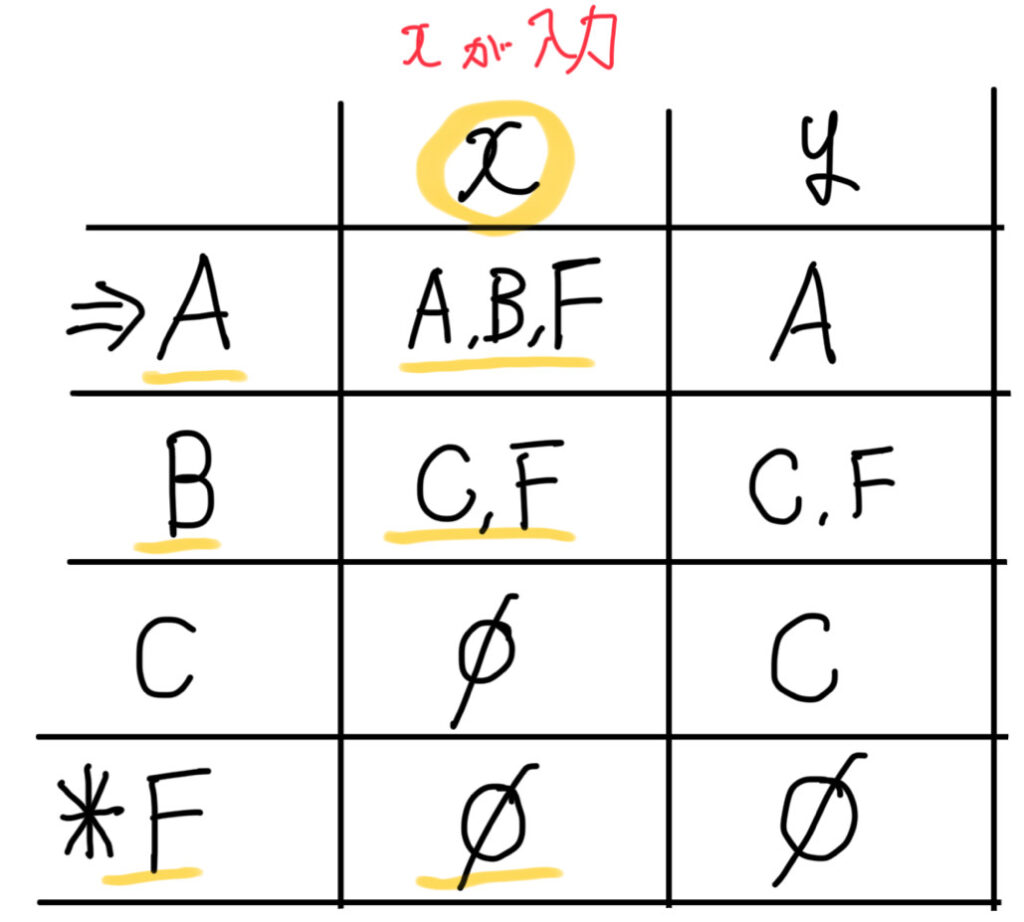
「A,B,F」で「y」が入力されたときを考えます。
「A」の時「y」が入力されると「A」に遷移。
「B」の時「y」が入力されると「C,F」に遷移。
「F」の時「y」が入力されると「Φ」。
したがって、「A,B,F」は「y」が入力されると「A,C,F」に遷移します。
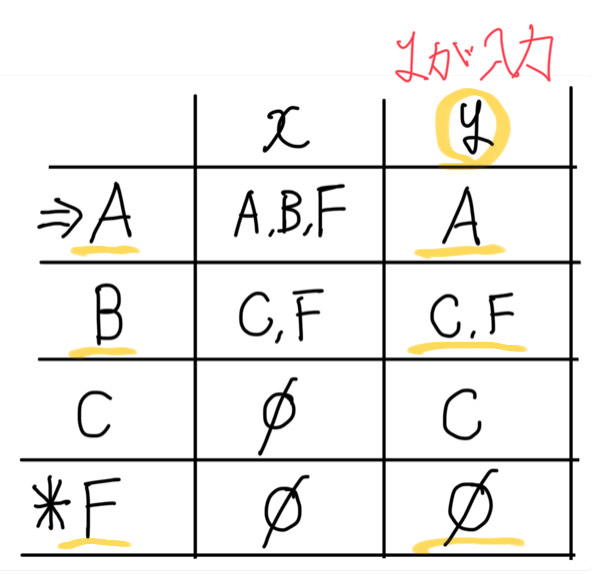
DFA状態遷移図の途中経過は↓のとおりになります。
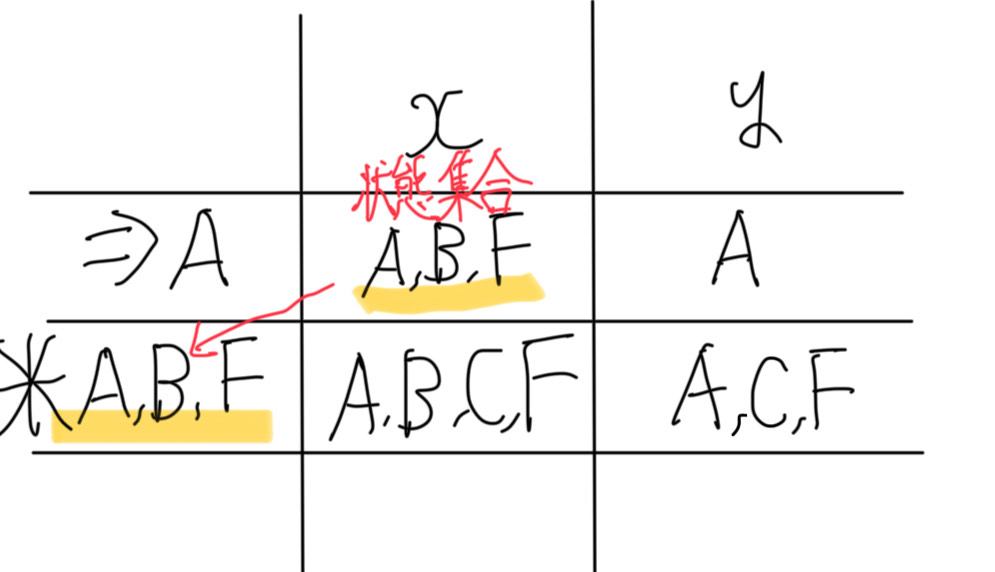
「A,B,F」の遷移先がきまりました。
次は、「A,B,F」がxが入力された時の状態集合「A,B,C,F」について考えます。
この状態は「A」「B」「C」「F」を集合として集めて考えた状態です。
なので、状態「A,B,C,F」で「x」が入力されると、「A」で「x」が入力された時の遷移先状態。「B」で「x」が入力された時の遷移先状態。「C」で「ｘ」が入力された時の遷移先状態。「F」で「x」が入力された時の遷移先状態 の集合として考えます。
「A」の時「x」が入力されると「A,B,F」に遷移。
「B」の時「x」が入力されると「C,F」に遷移。
「C」の時「x」が入力されると「Φ」
「F」の時「x」が入力されると「Φ」。
したがって、「A,B,C,F」は「x」が入力されると「A,B,C,F」に遷移します。
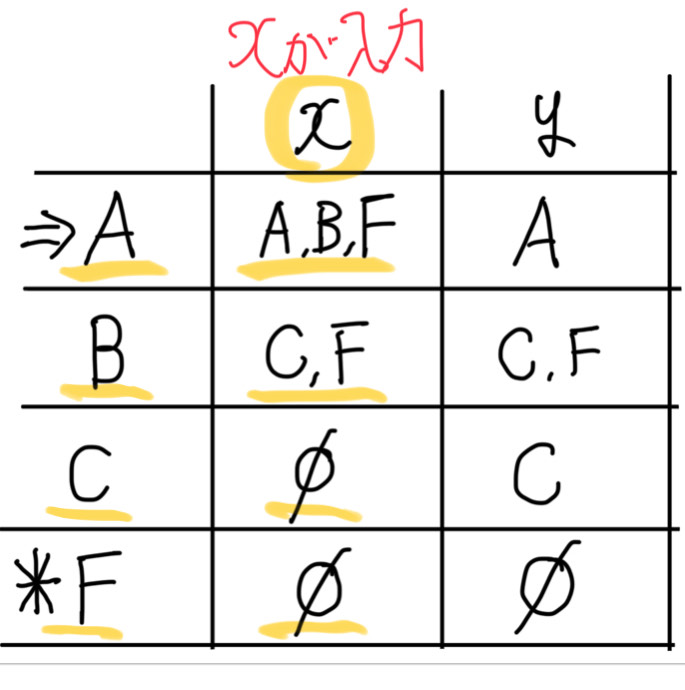
「A,B,C,F」で「y」が入力されたときを考えます。
「A」の時「y」が入力されると「A」に遷移。
「B」の時「y」が入力されると「C,F」に遷移。
「C」の時「y」が入力されると「Φ」。
「F」の時「y」が入力されると「Φ」。
したがって、「A,B,C,F」は「y」が入力されると「A,C,F」に遷移します。
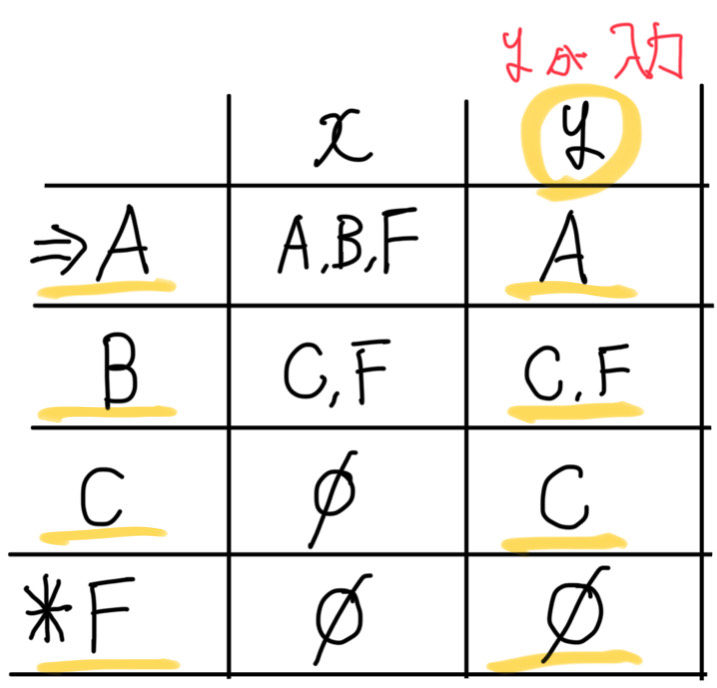
現在までの途中経過を↓の通りです。
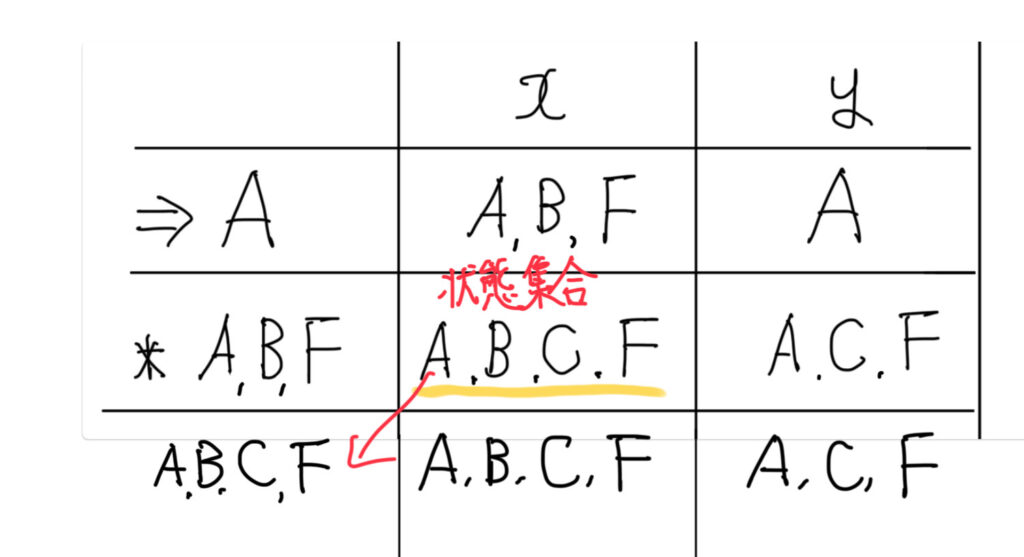
このような処理を続けることにより、
DFAの状態線遷移表を作成することができます。
DFA状態遷移表(完成形)
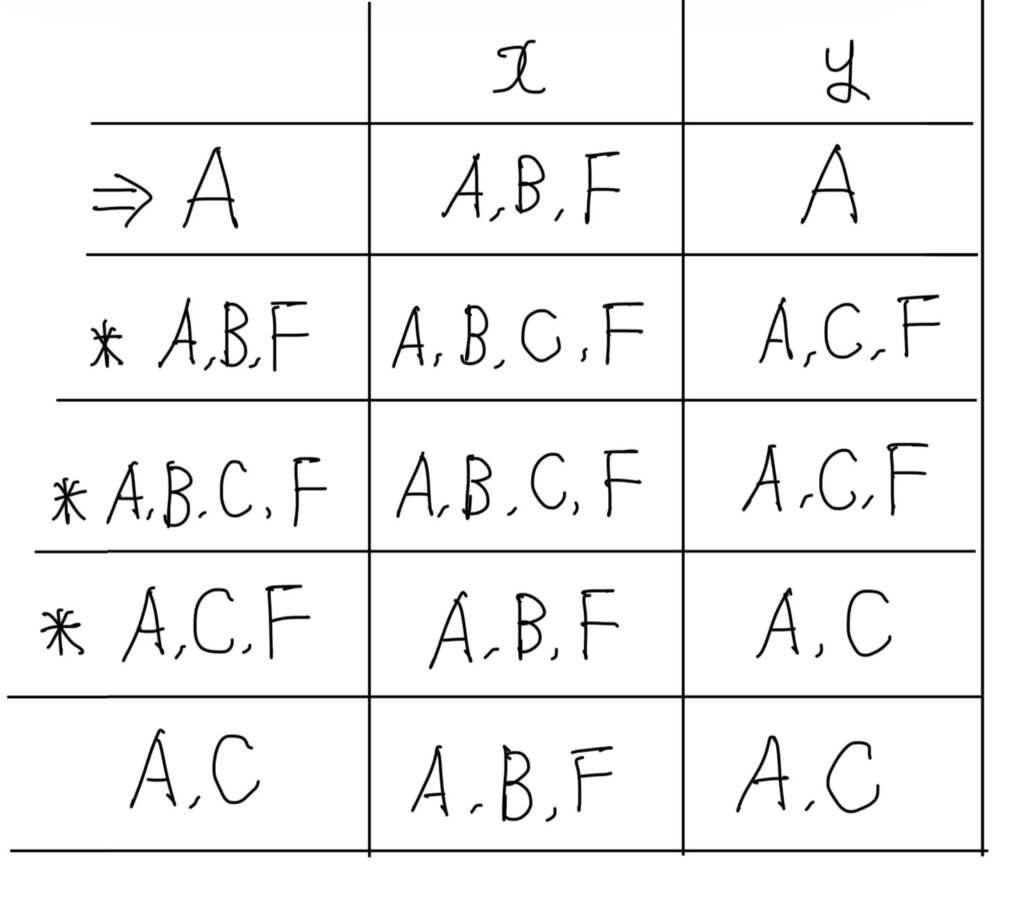
DFAの状態遷移表を作成しましたが、
状態集合を一つにまとめているので、「、」が入らなくても良いです。
※「A,B,F」などを「ABF」という表記させていただきます。
DFAの状態遷移表を図で表現すると
↓のようになります。
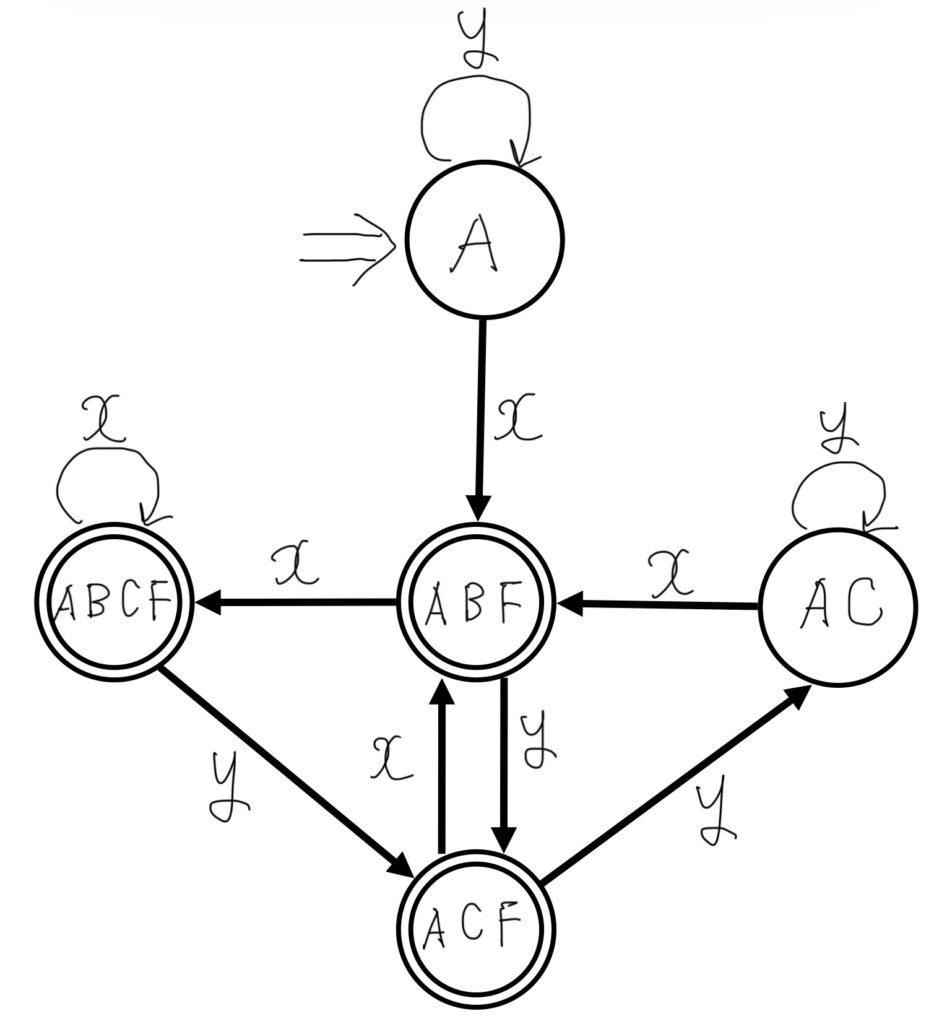
DFA→最簡形DFA
最後に
DFA(決定性有限オートマトン)を最簡形にした、最簡形DFAについて考えていきます。
最簡形DFAとは
与えられた言語を受理する全てのDFAの中で最も少ない状態数を持つDFAのことを指します。
〇最簡形を求める手順
１.状態を2つのグループに分る
２.グループを細分化
3.細分化できなくなるまで続ける
4.同値状態をまとめる
以上の処理をすることにより、最簡形にすることができます。
さきほどのDFAを用いて確認していきます。
1．状態を2つのグループに分ける
DFAの状態遷移表にある状態をグループ分けします。
最初は「受理状態」か「非受理状態」の２つのグループに分けます。
さきほどのDFAだと、状態は「A」、「ABF」、「ABCF」、「ACF」、「AC」
の5種類の状態があります。これらを2つのグループに分けます。
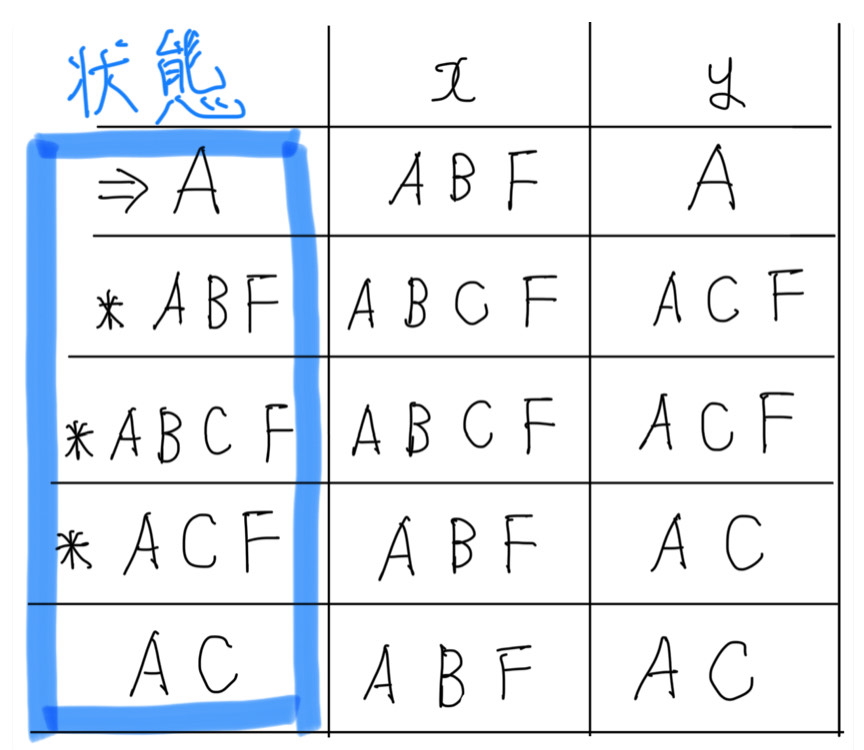
「*」がついているものが受理状態ですので、
非受理状態：「A」、「AC」
受理状態 ：「ABF」、「ABCF」、「ACF」
と分けることができます。
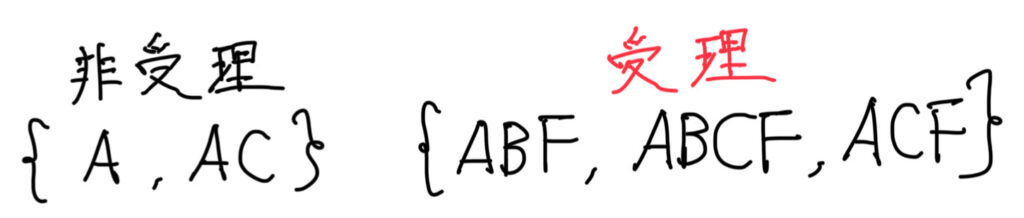
２．グループを細分化
グループを2つに分けたら、次はグループをより細かく分けていきます。
細分化する方法は、ある入力で遷移する先が異なるグループに属する場合、その状態を別のグループに分けるとい分け方です。
実際に先ほどのDFAを用いて確認していきます。
まずは、非受理グループから確認していきます。
非受理グループは「A」「AC」の2種類です。
「A」は「ｘ」が入力されたとき、「ABF」(受理グループ)に遷移します。
「A」は「ｙ」が入力されたとき、「Ａ」(非受理グループ)に遷移します。
「AC」は「ｘ」が入力されたとき、「ABF」(受理グループ)に遷移します。
「AC」は「ｙ」が入力されたとき、「AC」(非受理グループ)に遷移します。
非受理グループはどちらの状態も
「x」が入力されたら受理グループ
「y」が入力されたら非受理グループ
に遷移することがわかります。
というこで、今のところこれ以上グループを細分化することができません。
次は受理グループを確認していきます。
受理グループは、「ABF」「ABCF」「ACF」の3種類です。
「ABF」は「x」が入力されたとき、「ABCF」(受理グループ)に遷移します。
「ABF」は「y」が入力されたとき、「ACF」(受理グループ)に遷移します。
「ABCF」は「x」が入力されたとき、「ABCF」(受理グループ)に遷移します。
「ABCF」は「y」が入力されたとき、「ACF」(受理グループ)に遷移します。
「ACF」は「x」が入力されたとき、「ABF」(受理グループ)に遷移します。
「ACF」は「y」が入力されたとき、「AC」(非受理グループ)に遷移します。←ここだけ仲間はずれ
まとめてみると
「ABF」「ABCF」は
「x」が入力されたら受理グループ
「y」が入力されたら受理グループ に遷移しますが、
「ACF」は
「x」が入力されたら受理グループ
「y」が入力されたら非受理グループ に遷移します。
この場合は、「ABF」「ABCF」と「ACF」の2つのグループに分けることができます。
3.細分化できなくなるまで続ける
{A,AC}{ABF,ABCF}{ACF}
の3グループに分けることができています。
この状態で細分化できるか確認します。
{A,AC}グループ
どちらも
「x」が入力されたら受理グループ
「y」が入力されたら非受理グループ
となるので、細分化なし
{ABF,ABCF}グループ
どちらも
「x」が入力されたら受理グループ
「y」が入力されたら受理グループ
となるので、細分化なし
{ACF}は1つしかないので細分化なし
ということで、これ以上細分化できないのでグループ分けは終了です。
４．同値状態をまとめる
最後に、同じグループの中で同値状態のものをまとめます。
同値状態とは、どちらの状態からも同じ入力列で同じ受理結果になる状態のことです。
また、最終的な挙動が同じ場合も省略されます。
これも、引き続いてさきほどのDFAで確認します。
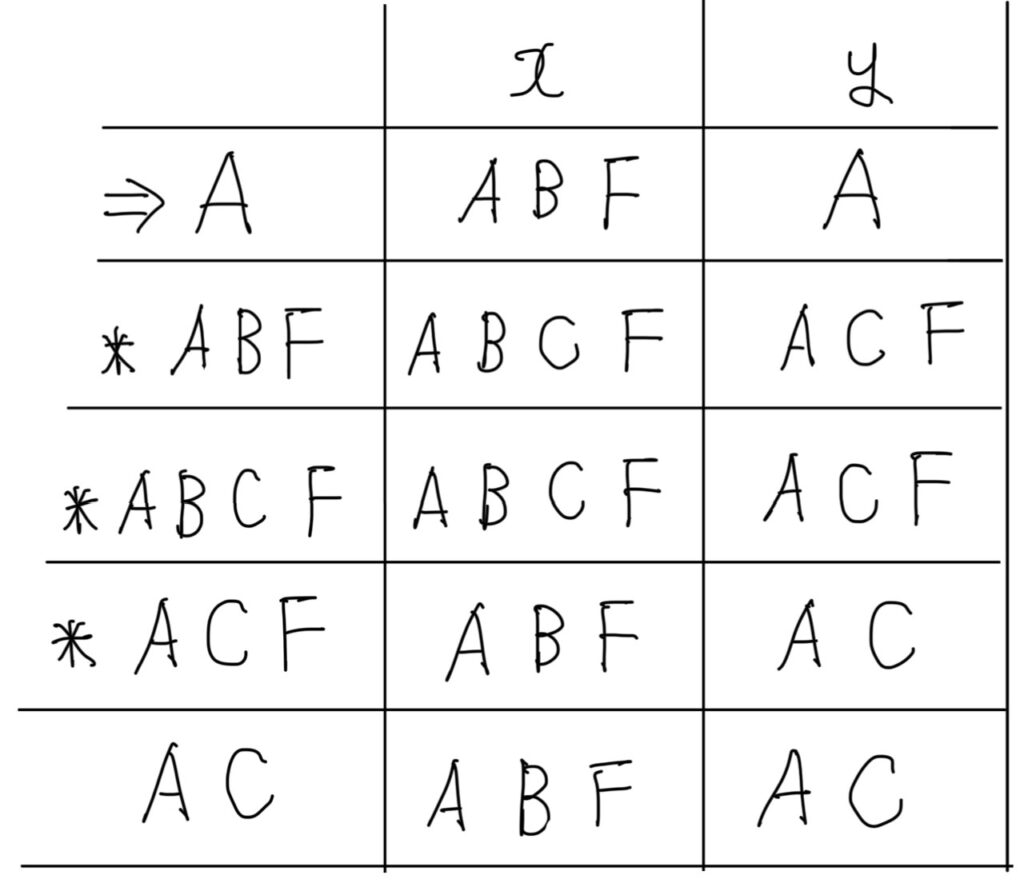
状態遷移表にグループ分けを対応させてみました。
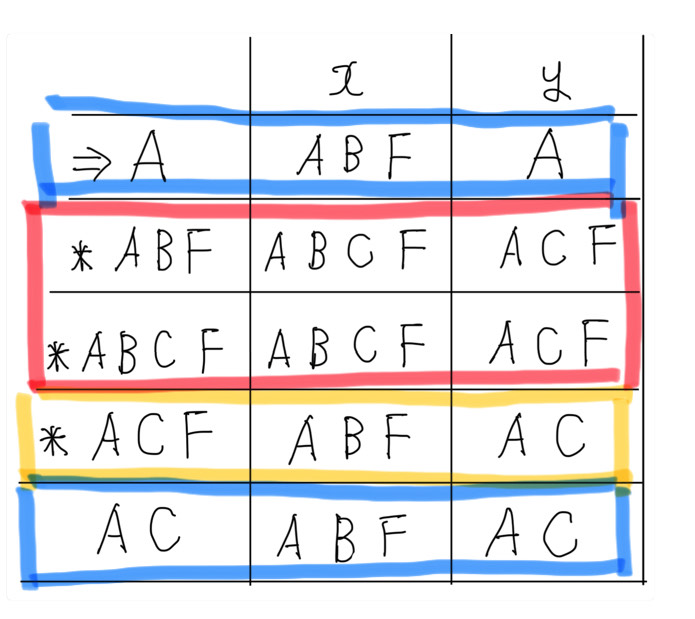
{ABF,ABCF}グループ
から確認していきたいと思います。
どちらも、受理状態である上に「x」「y」が入力されたときの遷移先が一緒です。
これは同値状態なので、一つにまとめることができます。
「ABF」→「ABCF」にすることができます。
状態遷移表で「ABF」の行を削除して、
表の中で「ABF」となっているところを「ABCF」に書き直すだけで大丈夫です。
↓のような表に変わると思います。
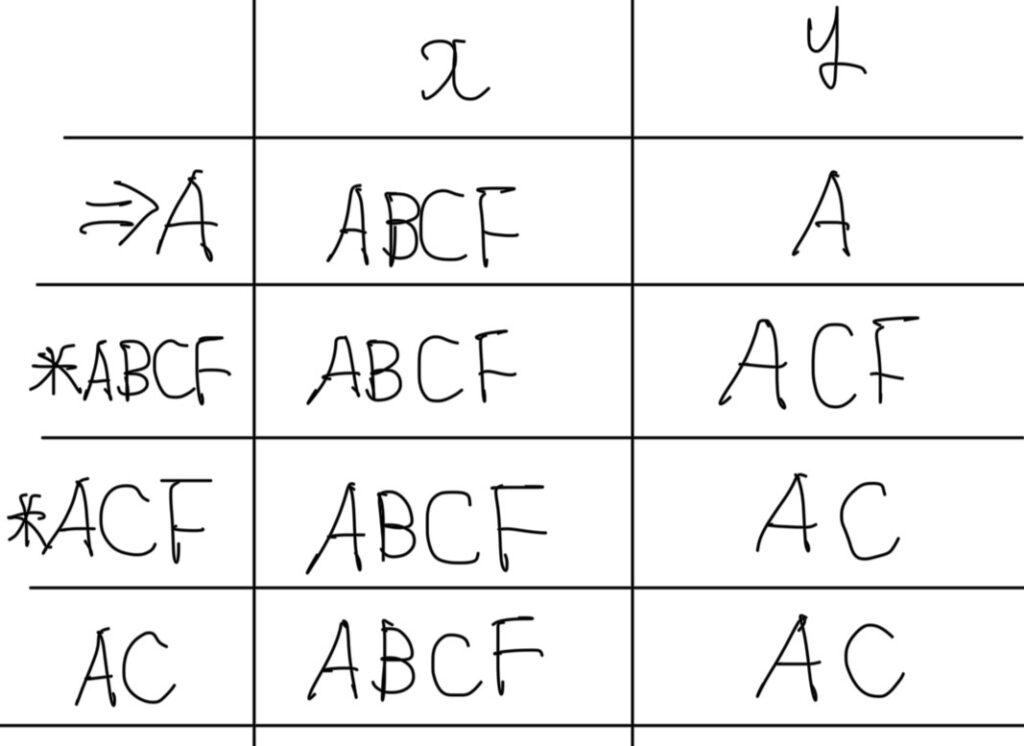
{A,AC}グループ
を確認します。
この2つは「ｘ」が入力されたときはどちらも「ABCF」へ遷移しますが、
「y」が入力されたときは異なる状態に遷移します。
一見すると、一つにまとめることができないように思えますが、最終的な挙動が同じなので
この場合も一つにまとめることができます。
比較してみるとわかりますが、「A」と「AC」の挙動はほぼ一緒です。
「A」「AC」に「x」が入力されるとどちらも受理状態である「ABCF」へ遷移します。
「A」「AC」に「y」が入力されるとどちらも自身へ遷移します。
このように、DFA内での役割は「A」「AC」同じであるので、
この場合は一つにまとめることができます。
先ほどと同じように、状態遷移表で「A」の行を削除して、
表の中で「A」となっているところを「AC」に書き直します。
また、「A」は初期状態の役割をもっていたので、「AC」に初期状態を継承させます。
状態遷移表はこのようになると思います。
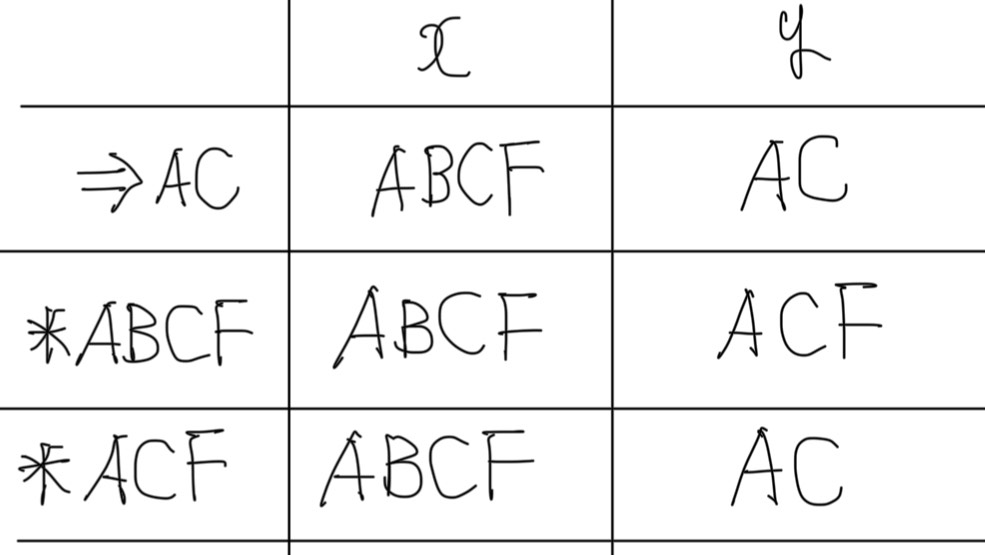
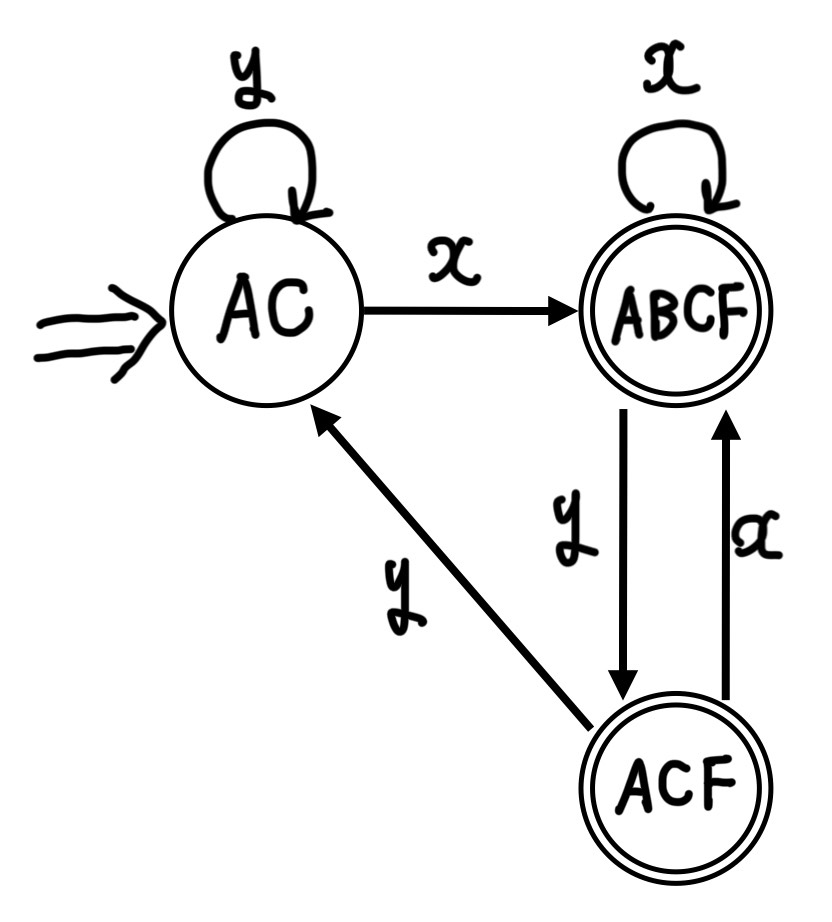
この最簡形のDFAの状態遷移表を図にしてみます。
↓のような状態遷移図になると思います。
これが最簡形決定性有限オートマトン(DFA)になります。
コメント