隣接行列とは?
隣接行列は、グラフをデータとして表現する場合に用いられ、節点同士で隣接する接点を表す行列。
※ここでのグラフとは、グラフ理論で用いられるグラフのことを指します。
グラフ理論では、節点(頂点)と線(辺)で表されるデータ構造をグラフと言います。
例)

このような、無向行列があったとします。
隣接する節点同士を表す行列なので、隣接行列は

となります。
隣接行列は、辺でつながっている隣接する節点を表す行列のため、
これは、各節点を1回だけ移動した場合、何処に移動できるかを表しているとも言えます。
隣接行列=「長さ1」の経路数(このグラフの場合「長さ1」の経路数は8である)
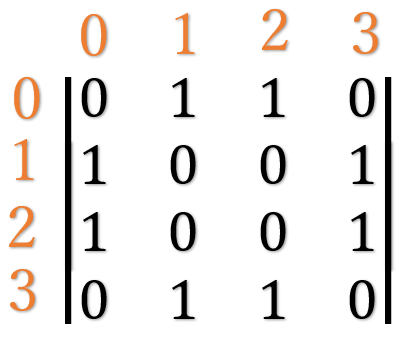
隣接行列の表記については、オレンジの数字が節点を示すとした場合、考えやすいです。
例えば、「節点0」を主人公として、「節点0」が1回だけ移動していけるのは、「節点1」か「節点2」だけです。
そのため、「1行目の2列目」と「1行目の3列目」は1が格納されています。
その他の、1行目は節点0から1回では移動できない節点は「0」と「3」のため「1行目の1列目」と「1行目の4列目」に0が格納されています。
2行目は、節点1が主人公で、節点1から1回の移動でどこにいけるかを表しています。
3、4行目も同じように考えます。
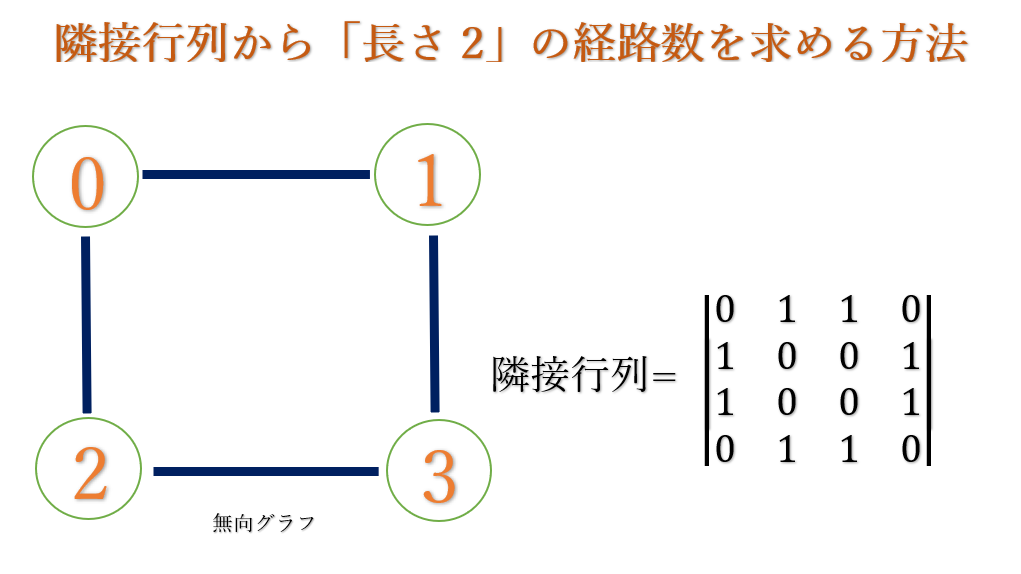
隣接行列から 「長さ2」 の経路数を求める方法
隣接行列とは何かがなんとなく理解できたところで、
例題を考えてみたいと思います。
Q)下の無向グラフで、ある節点から任意の節点への「長さ 2」 の経路の総数を求めよ

図1)無向グラフ
問題の ある節点から任意の節点への「長さ 2」 の経路というのは、
言い換えると、それぞれの節点が2回動いた場合、どの経路を通ることができきてそれの総数は何個ですかということになります。
先ほどの、隣接行列を作り出した時のように、主人公を節点0として、2回動いた場合どこに行くか、主人公節点1が2回動いた場合どこ行くか・・・のように1行1列ずつ求めても良いですが、隣接行列を使うことで効率的に「長さ2」の経路を求めることができます。
長さ2の経路数を表す行列 = 隣接行列 × 隣接行列で求めることができます。
これが、隣接行列がグラフをデータで表現する場合に用いられる理由なのです。
とても楽ちんですねー。これは、「長さ2」だけに限らず長さがいくつでも使うことができます。
長さ2の経路数を表す行列をCとして、隣接行列をAとします。
C=A×A
隣接行列Aは↓であったので、

長さ2の経路数を表す行列をCは、

で求めることができます。
行列Cは長さ2の経路数を表すので、 行列内にある数字の合計が長さ2の経路数の総数と言えます。
今回の場合だと、2が8コあるので、長さ2(2回動いた場合)の経路数は16通りということです。
隣接行列から 「長さ3」 の経路数を求める方法
前述したように、隣接行列を掛け合わせることで経路数を求める事ができます。
そのため、「長さ3」の経路数は隣接行列を3つ掛ければよいということです。
例えば、先ほどの例題で、「長さ3」の経路数を求めようとした場合、
C=A×A×A で求める事ができます。
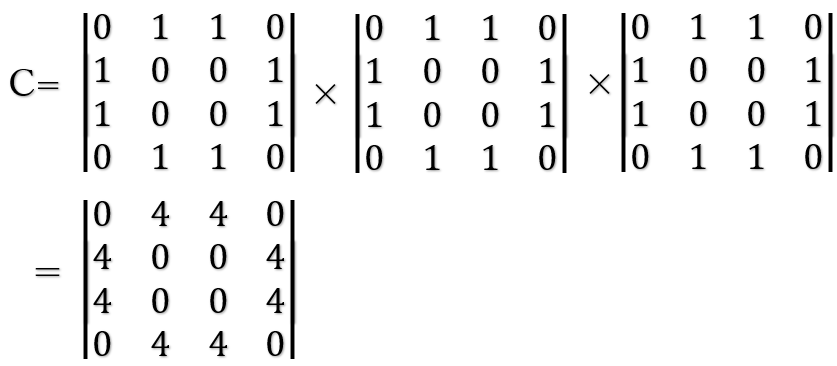
今回の場合だと、4が8コがあるため長さ3(3回動いた場合)の経路数は32通りということになります。

コメント