算術符号とは?
算術符号は、データ圧縮する方法の一つです。
(データ圧縮とは元のデータを別の符号に変換することにより全体を表現するバイト数を減らすこと)
算術符号:算術演算によって情報源記号全体を一つの符号語で符号化する可変長符号のこと
例えばA=2/3,B=1/3の情報源があったとします。
(Aが2/3の確率で、Bが1/3の確率で起こる事象)
情報源記号 Aを符号化した場合1つの符号で表現、
Aの次にBに起こる。情報源記号 AB を符号化した場合も1つの符号で表現、
Aの次にA が起こりBが起こる。情報源記号 AABを符号化した場合も1つの符号表現する
というように。どんな情報源記号を符号化した場合でも、1つの符号後で表すことが算術符号です。
また、算術符号の特徴は、全体を区間[0,1)で表し、符号化したものを区間内に対応させるところです。
算術符号の符号化
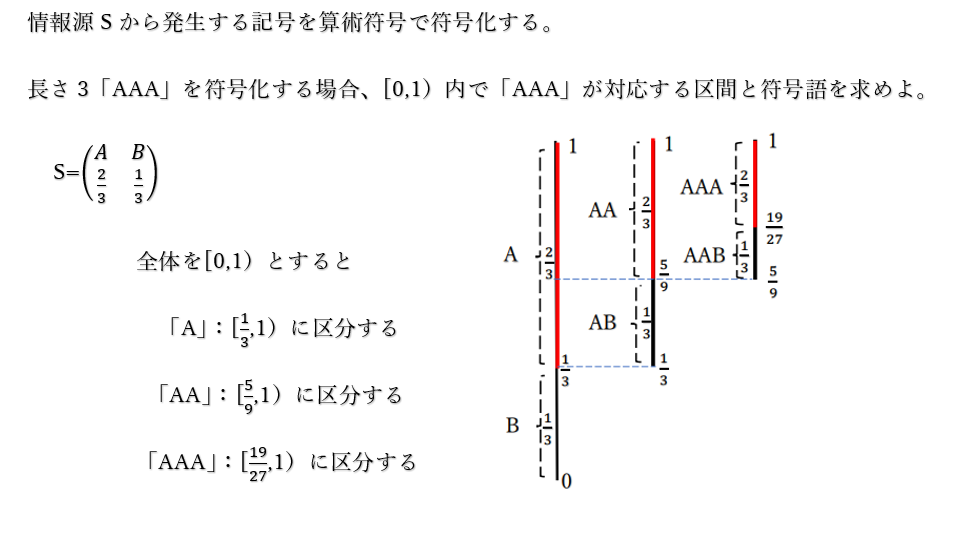
例えば次のような例題を考えます。
例題)


情報源Sから対応する区間は次のようになると考えられます。

この例題を用いて
算術符号の符号化を考えてみます。

とこのように
全体の区間内で、発生する記号を対応する区間に配置することが算術符号の符号化です。
同じ情報源Sについて、長さ3「AAB」が対応する区間と符号語も考えてみます。
「AA」までは先ほどと同様に行います。
「AA」の次に「B」が発生しています。



コメント
[…] […]