本記事は、情報理論の基礎である「情報源符号化」のまとめ記事シリーズの第3章です。
「情報源符号化」のまとめ記事では、「エントロピー」から始まり「条件付きエントロピー」「相互情報量」「通信路容量」「平均誤り率」「情報速度」について解説していきます。
統一した例題を使用しますので、ご安心して学んでいただけます。
第4章では「通信路容量」に焦点を当て、
その定義や意味、具体的な計算方法について解説します。
前回の「相互情報量」について解説した記事は↓になります。
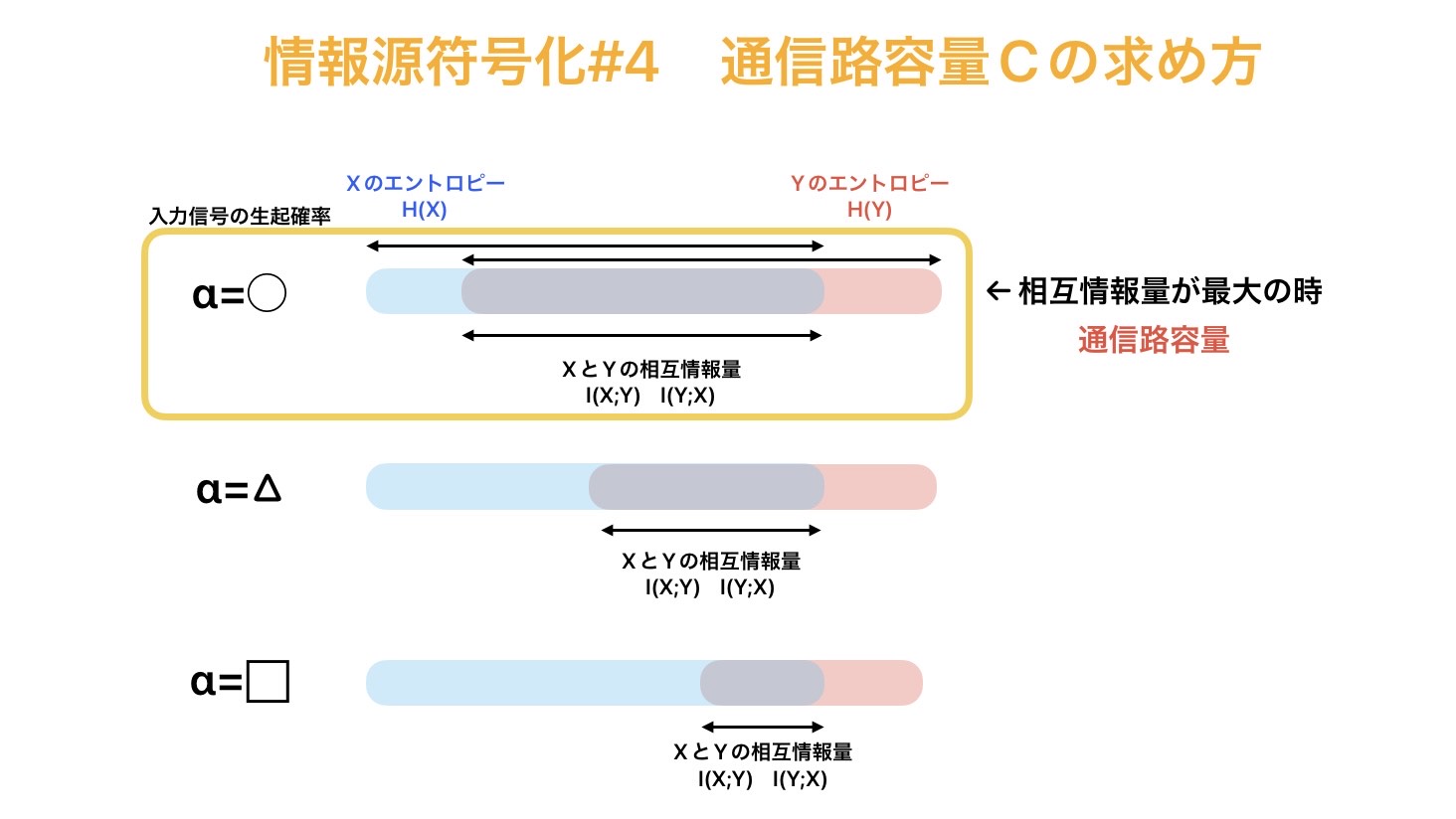
通信路容量とは?
通信路容量Cは一言でいうと、
「その通信路で理論的に送れる情報量の上限」
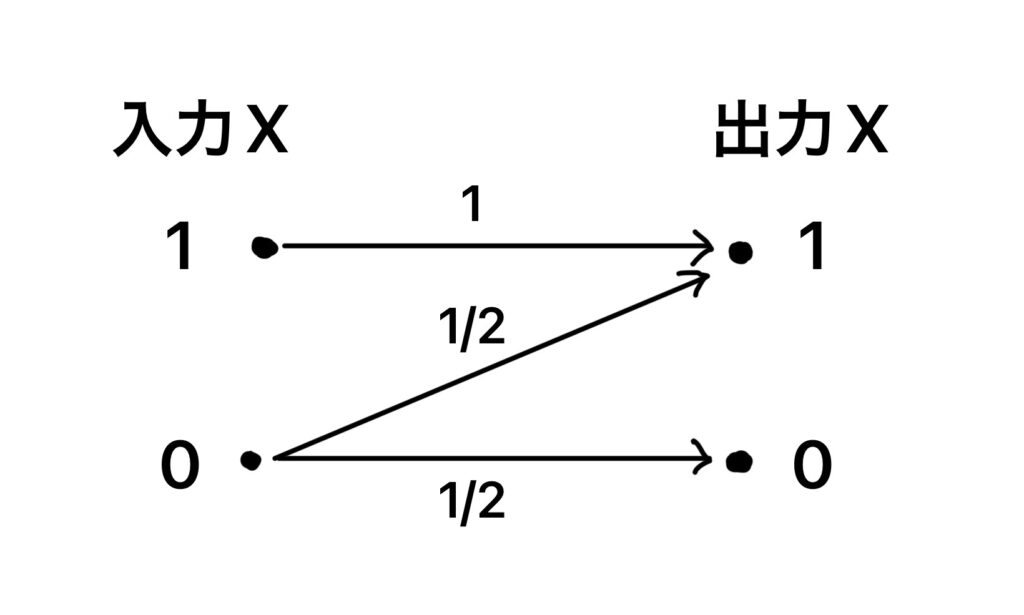
イメージしやすいように、図1の通信路を考える。
この通信路は
送信記号 0,1 を持つ。
この送信記号に対する生起確率をそれぞれ α1,α2として
送信側の確率分布α={α1,α2}と表す。
この通信路の通信路容量Cを式で表すと、
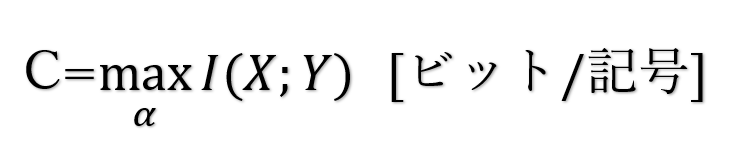
※ I(X;Y):相互情報量 (送信した情報Xから受信した情報Yの情報へ伝えられる情報量)
この式から、
情報通信路は相互情報量の最大値ということがわかる。
図でも確認する。
通信路の送信側をX、受信側をYとして、
先ほど同様に、送信側の確率分布α={α1,α2}と表す。
例として、α=〇の分布、α=△の分布、α=□の分布を考えてみると、
それぞれのαの分布に対応する、エントロピーの関係が存在する。
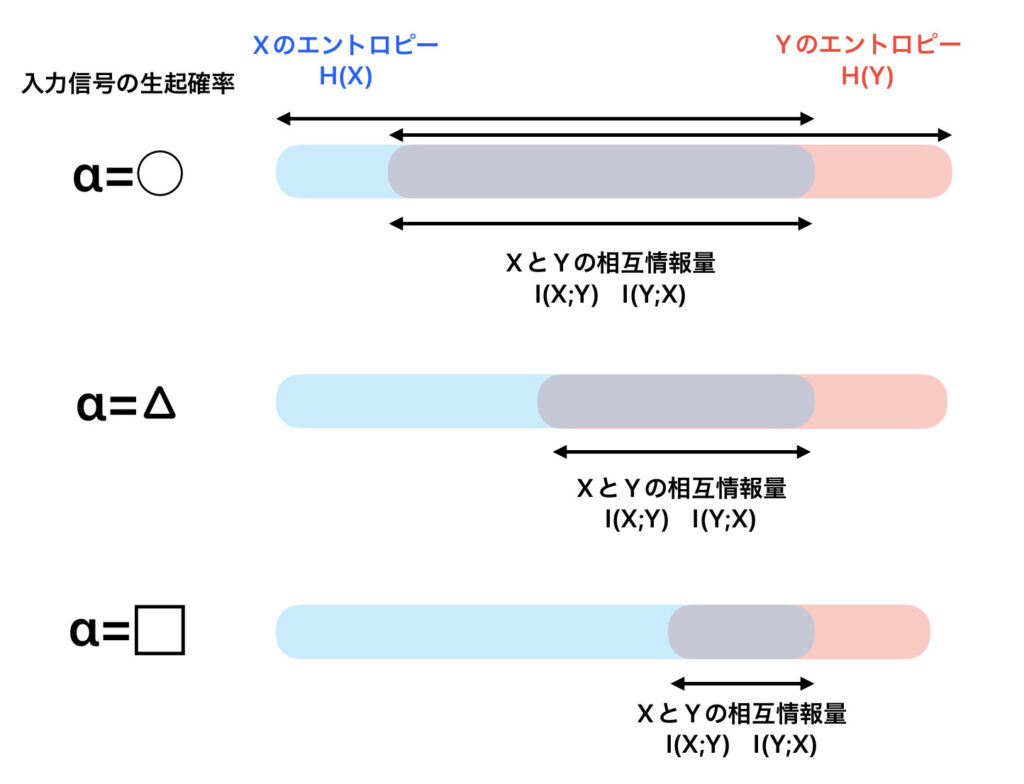
このエントロピーの関係で、
相互情報量I(X;Y) (図で言うと灰色の部分) が最大になるとき
この通信路において、
送信側から受信側へと理論的に送れる情報量の上限 といえる。
つまり、αの分布を最適化すれば、
相互情報量を最大化できるということ。
今回の例だと、α=〇分布の時がこの通信路においての通信路容量ということになる。

例題
[例題]
図のような2元無記憶通信路を考える。入力X,入力Yとし、いずれもアルファベット{0,1}上の確率変数であるとする。入力X=0となる確率をpとする。2元エントロピー関数h(α)=ーαlog2α ー (1ーα)log2(1ーα)を利用できる場合は、それを用いよ。
(1)エントロピーH(Y)を答えよ。 ←前回の記事#1で解説
(2)条件付きエントロピーH(Y|X)を答えよ。 ←前回の記事#2で解説
(3)相互情報量I(X;Y)を答えよ。 ←前回の記事#3で解説
(4)通信路容量C0とそれを実現するpの値をそれぞれ答えよ。←今回はココ
(5)2ビットの2元符号M={00,11}を考え、2つの符号語が1/2で生起する。
このとき、復号誤り率Pe(平均誤り率)を答えよ。
(6)(5)の2元符号の伝送速度R(情報速度)を答えよ。
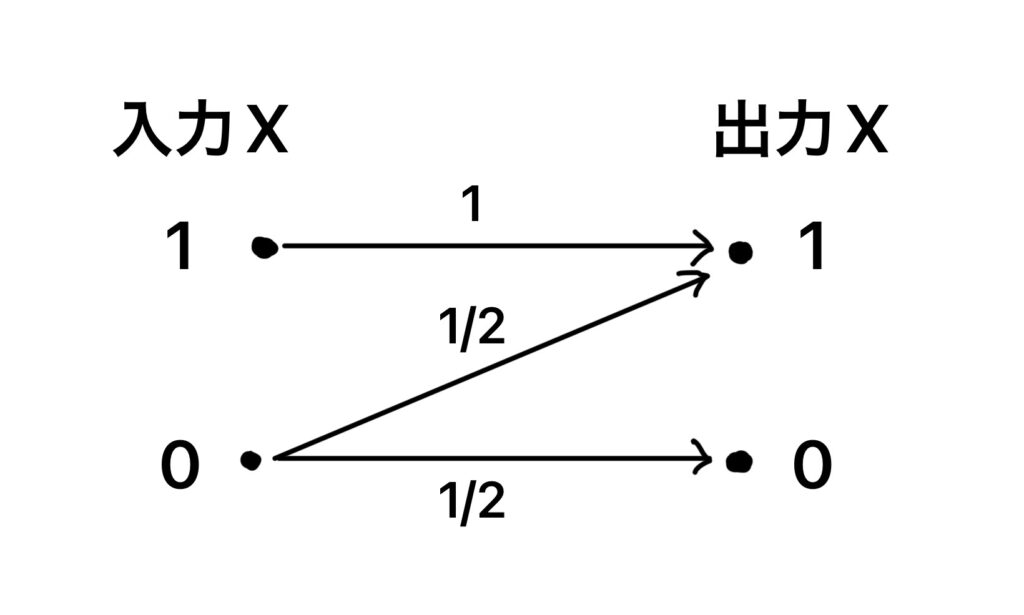
引用:名古屋工業大学 2021年度 大学院工学研究科(博士前期課程)
専門試験問題 (情報工学系プログラム)
解答
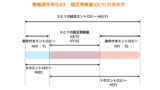
(4)通信路容量C0とそれを実現するpの値をそれぞれ答えよ。
I(X;Y)の最大値を求める。
I(X;Y)は(3)ですでに求めている。 ←前回の記事#3で解説
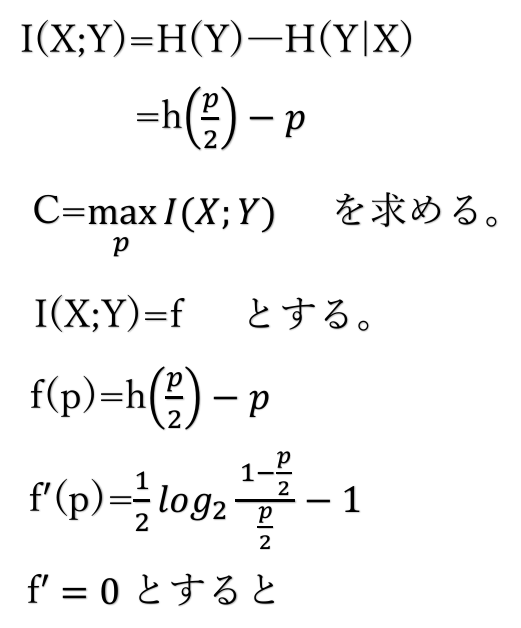
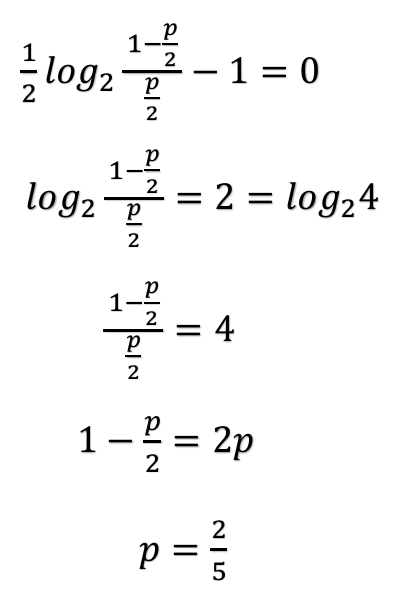

解説
(4)通信路容量C0とそれを実現するpの値をそれぞれ答えよ。
通信路容量は相互情報量が最大のときのこと。
相互情報量I(x;y)はpの関数となっているので、
この関数の最大値を微分を用いることで、
相互情報量の最大値つまり、通信路容量を求めることができる。


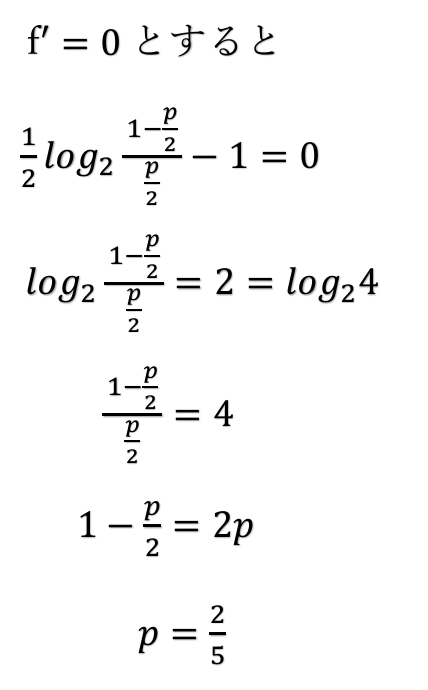



コメント